Flux estimate
The flux of scattered photons in an energy interval 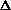 E and in a solid angle
E and in a solid angle 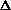
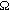 can be written as:
can be written as:
where No is the flux of the incident photons, 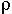 is the number of scattering units per unit volume, L is the sample length and
is the number of scattering units per unit volume, L is the sample length and 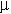 is the total absorption coefficient. The behaviour of the signal intensity as a function of atomic number in monatomic systems with an optimal sample length L=1/
is the total absorption coefficient. The behaviour of the signal intensity as a function of atomic number in monatomic systems with an optimal sample length L=1/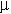 and f(Q)=Z is reported in figure below.
and f(Q)=Z is reported in figure below.
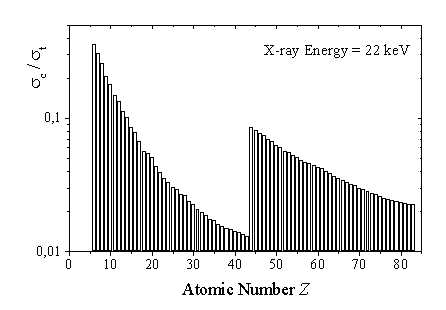
Ratio between the total number of photons scattered by the Thomson process and those lost through all the other processes (predominantly through photoelectric absorption) in a sample of optimum length 1/ as a function of the atomic number Z for an incident photon energy of 22 keV.
as a function of the atomic number Z for an incident photon energy of 22 keV.
We show the quantity  c/
c/ t, with
t, with  c=(roZ)2 and
c=(roZ)2 and  t=
t=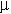 /
/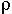 which provides a measure of the efficiency of the method for a given photon energy. The step between Z=44 and Z=45 signifies the energy of the K-shell absorption edge with respect to the incident photon energy (in this case 22 keV). If the photon energy is smaller than the K-shell binding energy, more sample can be probed, whereas in the other case an additional absorption channel opens up, and consequently the scattering volume is reduced. From the above said, it is obvious that low momentum transfer studies of disordered materials become increasingly difficult for large Z materials. For single crystal materials this limitation can be overcome by working in higher Brillouin zones, where the Q2-increase of the inelastic cross section partly compensates for the decrease of the f(Q).
which provides a measure of the efficiency of the method for a given photon energy. The step between Z=44 and Z=45 signifies the energy of the K-shell absorption edge with respect to the incident photon energy (in this case 22 keV). If the photon energy is smaller than the K-shell binding energy, more sample can be probed, whereas in the other case an additional absorption channel opens up, and consequently the scattering volume is reduced. From the above said, it is obvious that low momentum transfer studies of disordered materials become increasingly difficult for large Z materials. For single crystal materials this limitation can be overcome by working in higher Brillouin zones, where the Q2-increase of the inelastic cross section partly compensates for the decrease of the f(Q).



