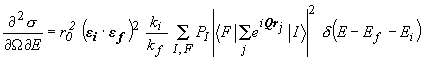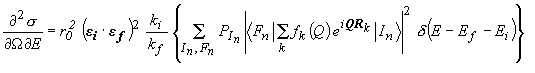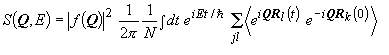- Home
- Users & Science
- Find a beamline
- Electronic structure, magnetism and dynamics
- ID28 - Inelastic Scattering II
- Introduction to IXS
- The Double Differential Cross Section
The Double Differential Cross Section
The double differential cross-section is proportional to the number of incident probe particles scattered within an energy range 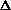 E and momentum variation into a solid angle
E and momentum variation into a solid angle 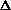
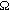 . In the process, where a photon of energy Ei, wavevector kI, and polarization
. In the process, where a photon of energy Ei, wavevector kI, and polarization 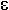 i, is scattered into a final state of energy Ef, wavevector kf , and polarization
i, is scattered into a final state of energy Ef, wavevector kf , and polarization 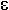 f , and the electron system goes from the initial state |I> to the final state |F>, we obtain:
f , and the electron system goes from the initial state |I> to the final state |F>, we obtain:
The sum over the initial and final states is the thermodynamic average, and PI corresponds to the thermal population of the initial state. From this expression, which implicitly contains the correlation function of the electron density, one arrives to the correlation function of the atomic density, on the basis of the following considerations: i) We assume the validity of the adiabatic approximation. This allows to separate the system quantum state |S> into the product of an electronic part, |Se>, which depends only parametrically from the nuclear coordinates, and a nuclear part, |Sn>: |S>=|Se>|Sn>. This approximation is particularly good for exchanged energies that are small with respect to the excitations energies of electrons in bound core states: this is indeed the case in basically any atomic species when considering phonon energies. In this approximation, one neglects the portion of the total electron density contributing to the delocalised bonding states in the valence band region. ii) We limit ourselves to consider the case in which the electronic part of the total wavefunction is not changed by the scattering process, and therefore the difference between the initial state |I>=|Ie>|In> and the final state |F>=|Ie>|Fn> is due only to excitations associated to atomic density fluctuations. Using these two hypotheses we then obtain:
where fk(Q) is the atomic form factor of the atom k and Rk its position vector. The expression in the curly brackets contains the dynamical structure factor S(Q,E). Assuming that all the scattering units in the system are equal, this expression can be simplified by the factorisation of the form factor of these scattering units:
where N is the number of atoms in the system. The brackets indicate the thermal average. In this presentation, S(Q,E) is the space-and time Fourier transform of the pair correlation function Gp(R,t), which is identified with the probability to find two different particles at positions Rk(0) and Rl(t), separated by the distance r and at different times t. The double differential cross section can then be written as:
(1)
For this specific case, the coupling characteristics of the photons to the system, the Thomson scattering cross section, is separated from the dynamical properties of the system, and the atomic form factor f(Q) appears only as a multiplicative factor. The corresponding INS cross section is obtained by replacing the Thomson cross section and the atomic form factor by the coherent neutron scattering length b of the element under study. For this specific case, INS and IXS both probe the S(Q,E) in the same fashion.
As already mention above, the cross-section of equation (1) is valid for a system composed of a single atomic species. This derivation, however, can be easily generalised to molecular or crystalline systems by substituting the atomic form factor with either the molecular form factor, or the elementary cell form factor, respectively. This is in close analogy to INS, although the different atom species contribute differently to the S(Q,E) for neutrons and X-rays. This arises from the fact that both the Q-dependence and the atomic number, Z, dependence of the X-ray form factor and of the neutron scattering length are substantially different. The situation becomes more involved if the system is multi-component and disordered. In this case the factorisation of the form factor is still possible only assuming some distribution among the different atoms. In the limit case that such distribution is completely random, an incoherent contribution appears in the X-ray scattering cross-section3.
The functional form of the S(Q,E) depends on whether the system is crystalline or amorphous. In the first case, the formalism for phonons is well established. The inelastic structure factor, symmetry considerations, and phonon selection rules are identical to the one for INS. For a detailed description the interested reader is referred to the chapter dedicated to INS and standard text books7,8. For amorphous systems one has to extend the macroscopic hydrodynamic theory in order to properly take into account that the wavelength of the probing particle approaches interatomic distances and to include eventual relaxation processes. This is subject of the so-called generalised hydrodynamic theory3. One of the most common methods to derive this generalisation is to introduce the concept of memory functions.
3. U. Balucani and M. Zoppi, “Dynamics of the Liquid State”, Oxford Science Publ., Oxford, (1994).
7. S.W. Lovesey, “Theory of Neutron Scattering from Condensed Matter”, Clarendon Press, Oxford (1984).
8. B. Dorner in “Coherent Inelastic Neutron Scattering in Lattice Dynamics”, Springer, Berlin (1982).