- Home
- News
- Spotlight on Science
- Getting smaller...
Getting smaller and smaller: Coherent microdiffraction imaging to retrieve shape and local strain of a single nanocrystal
10-05-2006
Nanoscience aims at understanding the properties of materials, which change when the sample size reaches the nanometre scale. For the physical properties of nanocrystals, an important role is played not only by the size, but also by the strain distribution, which is strongly affected by the presence of surfaces and interfaces. Coherent diffraction imaging provides a destruction-free tool to access the structure directly from the scattering pattern and is thus model-independent.
The high brilliance of third-generation synchrotron sources has allowed great advances in the imaging of nanomaterials. It has recently been proven that the complete 3D shape of an object can be directly reconstructed from its over-sampled coherent X-ray diffraction pattern, i.e. that the "phase problem" can be solved [1]. This method is promising for the study of a single strained nanocrystal, if two major restrictions can be solved: (i) the previously applied iterative algorithms are modified in order to reconstruct a complex-valued object with a modulus 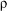 (
( 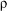 being the density) and a phase
being the density) and a phase 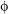 = G. u (where G is the reciprocal lattice vector and u is the displacement field) and (ii) the coherent flux impinging on the sample is increased since the coherently diffracted intensity decreases with the square of the particle volume.
= G. u (where G is the reciprocal lattice vector and u is the displacement field) and (ii) the coherent flux impinging on the sample is increased since the coherently diffracted intensity decreases with the square of the particle volume.
In an experiment recently carried out at ESRF's beamline ID01 both conditions have been met. The evaluation of the diffraction pattern yields shape and strain distribution in a single 120 nm small ZrC nanocrystal with a spatial resolution of about 10 nm.
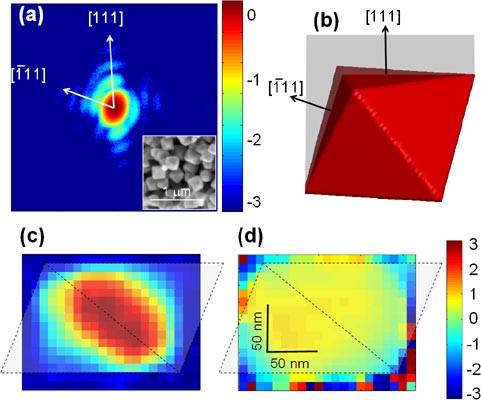
We used a 1x1 mm2, 9.5 keV X-ray beam and focused it to 8x3 µm2 by 31 Be compound refractive lenses onto a 120 nm sized ZrC octahedron shaped nanocrystal (see inset of figure (a)). When compared to an unfocused beam of the same size, the gain in coherent flux was about 3*103. Under these conditions, the coherent diffraction pattern from the (111) reflection were recorded by a directly illuminated CCD, accumulating 1700 frames of 2 s each (figure (a)). Three fringes with an angle of 71° along the [111] and [-111] directions, resulting from the octahedron facets, exhibit a dynamic range of about 103. The 2D intensity pattern corresponds to the diffraction of the 2D projection of the octahedron on the (01-1) plane as shown in grey in figure (b). We have developed a modified iterative algorithm by which 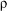 and
and 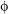 can be reconstructed as shown in figures (c) and (d). The resolution of about 10 x 10 nm2 is reached and indicated by the small squared pixels on both maps. The edge of the projected octahedron is outlined as dashed lines as a guide to the eye. The 2D modulus is related to the projection of the crystal's density on the (01-1) scattering plane and the phase is directly related to the deformation: while the core of the particle is rather unstrained (constant
can be reconstructed as shown in figures (c) and (d). The resolution of about 10 x 10 nm2 is reached and indicated by the small squared pixels on both maps. The edge of the projected octahedron is outlined as dashed lines as a guide to the eye. The 2D modulus is related to the projection of the crystal's density on the (01-1) scattering plane and the phase is directly related to the deformation: while the core of the particle is rather unstrained (constant 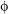 ), a phase shift is observed in the near surface region corresponding to a strain of about 8*10-4. Numerical simulations of the shape as well as transmission electron microscopy investigations further confirm the result of the inversion. Work is in progress to reveal the origin of the strain field.
), a phase shift is observed in the near surface region corresponding to a strain of about 8*10-4. Numerical simulations of the shape as well as transmission electron microscopy investigations further confirm the result of the inversion. Work is in progress to reveal the origin of the strain field.
References
[1] Miao et al., Phys. Rev. Lett. 89, 088303 (2002); G.J. Williams et al., Phys. Rev. Lett. 90, 175501 (2003).
Authors
V. Chamard (a,d), M. Dollé (b), G. Baldinozzi (c), F. Livet (d), M. de Boissieu (d), F. Bley (d), P. Donnadieu (d), T.H. Metzger (e), C. Mocuta (e), F. Picca (f), S. Labat (a) and O. Thomas (a).
(a) TECSEN, UMR CNRS 6122, Université Aix-Marseille III (France)
(b) CEA Saclay DEN/DANS/DMN/SRMA/LA2M (France)
(c) SPMS-Ecole Centrale Paris (France)
(d) LTPCM, UMR CNRS 5614, ENSEEG/INPG Saint Martin d'Hères (France)
(e) ESRF
(f) Soleil, Gif-sur-Yvette (France)