- Home
- Users & Science
- Scientific Documentation
- ESRF Highlights
- ESRF Highlights 2012
- Structure of materials
- An alternative pathway for understanding plasticity at the micrometre scale
An alternative pathway for understanding plasticity at the micrometre scale
The flow stress of a material, being the stress where a permanent change in sample shape occurs, inherently depends on the chemical composition and the microstructure of the material, including also the density and type of lattice defects. From a classical point of view, the flow stress should not depend on the geometrical sample dimensions. This assumption, believed valid for centuries and used as a fundamental basis of design in mechanical engineering, was proven to be incorrect less than a decade ago. Uchic and co-workers [1] have reported on the tremendous increase of the flow stress when sample sizes are reduced and reach micrometre or even submicrometre dimensions. This size effect is not only interesting from a scientific point of view, but also a challenge for future developments. The ongoing trend in miniaturisation – for instance in microelectronics – requires a thorough understanding of the material properties at this length scale.
The reason for the unexpected increase in flow stress is, however, not fully understood. Advanced techniques in materials science, like in situ scanning electron microscopy (SEM, see Figure 135) or transmission electron microscopy (TEM) have been applied to small scale samples but have not completely shed light on the fundamental mechanisms increasing the strength. Thus, alternative pathways like in situ µLaue diffraction are needed and have been applied successfully at beamline BM32 (CRG-IF).
 |
|
Fig. 135: SEM image of a micrometre sized single crystalline copper pillar deformed at BM32 with slip steps only on one {111} crystallographic plane. |
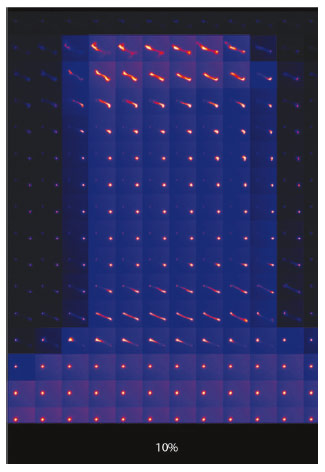
Compression, bending, and tensile samples ranging from 3 to 10 µm in diameter were produced from macroscopic single crystalline copper using focused ion beam milling (FIB). Subsequently, the samples were loaded in displacement controlled mode with a force resolution of typically 10 µN. During loading, a 1 µm sized polychromatic X-ray beam was focussed on the sample allowing for an in situ characterisation of microstructural changes like crystal rotations, formation of deviatoric strains and dislocation structures. The site specific investigations of the dislocation densities were used to link the defect structure to the mechanical response of the material. Furthermore, raster scanning as presented in Figure 136 leads to a global image of dislocation storage across the entire sample. In regions with a high density of excess dislocations the diffraction spot is elongated (i.e. “streaked”), whereas in regions with low excess dislocation content the peak appears circular.
 |
|
Fig. 136: Corresponding map of the (111) Laue spot across the entire sample. In the sample base (bottom) and in the sample centre the Laue spot appears circular (no excess dislocations), whereas at the top and the end of the gauge section the spot is streaked, indicating the storage of excess dislocations on the primary slip system. |
In the underlying studies, we demonstrated the severe impact of sample misalignments on the storage of excess dislocations in micrometre sized compression pillars [2], the critical influence of the initial dislocation source size statistics onto the deformation behaviour at the micrometre scale during tensile testing [3] and, finally, the reversibility of dislocation movement in bending beams due to internal stress fields [4].
Principal publication and authors
C. Kirchlechner (a,b), C. Motz (b), P.J. Imrich (a), W. Liegl (b), J. Keckes (b), O. Thomas (c), S. Labat (c), J.S. Micha (d,e), O. Ulrich (d,e) and G. Dehm (a,b), Acta Materialia 60, 1252–1258 (2012).
(a) Department of Materials Physics, Montanuniversität Leoben (Austria)
(b) Erich Schmid Institute of Materials Science, Austrian Academy of Sciences (Austria)
(c) Aix-Marseille Université, CNRS, IM2NP UMR 7334 (France)
(d) CEA-Grenoble/Institut Nanosciences et Cryogénie (France)
(e) CRG-IF BM32 at ESRF (France)
References
[1] M.D. Uchic, D.M. Dimiduk, J.N. Florando and W.D. Nix, Science 305, 986 (2004).
[2] C. Kirchlechner, J. Keckes, C. Motz, W. Grosinger, M.W. Kapp, J.S. Micha, O. Ulrich and G. Dehm, Acta Materialia 59, 5618 (2011).
[3] C. Kirchlechner, P.J. Imrich, W. Grosinger, M.W. Kapp, J. Keckes, J.S. Micha, O. Ulrich, O. Thomas, S. Labat, C. Motz and G. Dehm, Acta Materialia 60, 1252 (2012).
[4] C. Kirchlechner, W. Grosinger, M.W. Kapp, P.J. Imrich, J.S. Micha, O. Ulrich, J. Keckes, G. Dehm and C. Motz, Philosophical Magazine 92, 3231 (2012).



