- Home
- Users & Science
- Scientific Documentation
- ESRF Highlights
- ESRF Highlights 2000
- Soft Condensed Matter
- Ordering Phenomena in Confined Fluids
Ordering Phenomena in Confined Fluids
From everyday experience we know that a fluid film between two solid surfaces acts as a lubricant. Examples are fluids of alkanes, solutions of nanoparticles (e.g. MoS2) or granular systems such as clays. It is well known that the lubricating properties of the film strongly depend on its thickness, i.e. the degree of confinement. As the gap between the confining surfaces decreases to a few molecule or particle diameters, the confined fluid is generally found to become stickier. This confinement effect has been attributed to a solid-like ordering of the constituents of the fluid in layers parallel to the confining surfaces [1]. However, such layering has not yet been put into direct experimental evidence.
We have developed a novel coherent X-ray scattering method for probing ordering phenomena in confined fluids. The method makes use of the waveguiding properties of the gap between the confining plates. The principle is illustrated in Figure 32 for two parallel plates with adjustable gap width, confining a suspension of colloidal silica particles. The X-ray beam is directed into the gap along a direction nearly parallel to the plates. Interference between the incident and reflected waves at the entrance gives rise to a standing wave pattern ('waveguide modes'), which can be made to fit exactly within the gap by adjustment of the angle of incidence or the gap width. Within the plate material, the wavefield decays rapidly to zero. If the fluid were absent, the waveguide modes would propagate undisturbed through the gap. In the filled waveguide, however, the spatial variations in the electron density of the fluid give rise to scattering into other waveguide modes ('mode coupling'). The distribution of intensity over the different modes is observed in Fraunhofer diffraction patterns of the wavefield across the waveguide's exit plane. From these, the density profile is determined through a model-dependent analysis.
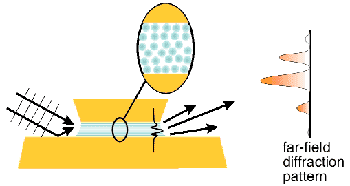 |
Fig. 32: Schematic of the waveguiding geometry (not to scale). The fluid within the gap has ordered into layers parallel to the plates. The incident wavefield is scattered from the layered density distribution into several waveguide modes. The distribution of intensity over these modes gives rise to a characteristic diffraction pattern in the far field, from which the density profile of the fluid across the gap can be derived.
|
Here we show data for a 10 vol.% suspension of colloidal silica particles (Ø 110 nm) in dimethylformamide, confined within a gap of 655 nm. The waveguiding experiment was performed at ID10A, at a wavelength of 0.093 nm. Figure 33 shows a contour plot of the diffracted intensity I(![]() i,
i,![]() e), measured as a function of the incidence angle
e), measured as a function of the incidence angle ![]() i and the exit angle
i and the exit angle ![]() e. The intense off-diagonal peaks are evidence of strong mode coupling. The same measurements for the waveguide without fluid (not shown) yield only modes along the diagonal [2]. Calculations of the intensity distributions for various models of the density profile show agreement with the data for a filling of the gap with six layers, see the bottom panels of Figure 33. The measurements strongly suggest that the confinement induces a crystallisation in a closed-packed arrangement of the particles. Similar results were obtained for a gap of 310 nm, which confined two crystallised layers.
e. The intense off-diagonal peaks are evidence of strong mode coupling. The same measurements for the waveguide without fluid (not shown) yield only modes along the diagonal [2]. Calculations of the intensity distributions for various models of the density profile show agreement with the data for a filling of the gap with six layers, see the bottom panels of Figure 33. The measurements strongly suggest that the confinement induces a crystallisation in a closed-packed arrangement of the particles. Similar results were obtained for a gap of 310 nm, which confined two crystallised layers.
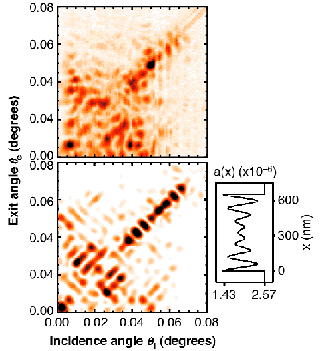 |
Fig. 33: Contour plot of the diffracted intensity I(
|
Our method can be modified so as to include studies of (molecular) fluids confined within much smaller gaps. One should then make use of multi-step index waveguides and detect both guided and radiative modes.
References
[1] B.N.J. Persson, Sliding Friction, Springer (1998).
[2] M.J. Zwanenburg, J.H.H. Bongaerts, J.F. Peters, S.A. de Vries, D.L. Abernathy and J.F. van der Veen, Phys. Rev. Lett. 82, 1696 (1999).
Principal Publication and Authors
M.J. Zwanenburg (a), J.H.H. Bongaerts (a), J.F. Peters (a), D.O. Riese (a) and J.F. van der Veen (b), Phys. Rev. Lett. 85, 5154 (2000).
(a) University of Amsterdam (The Netherlands)
(b) Paul Scherrer Institut, Villigen (Switzerland)



