- Home
- Users & Science
- Scientific Documentation
- ESRF Highlights
- ESRF Highlights 2000
- Magnetism
- Orbital Magnetic Moment Instability at the Spin Reorientation Transition of Nd2Fe14B
Orbital Magnetic Moment Instability at the Spin Reorientation Transition of Nd2Fe14B
One of the most interesting problems in magnetism that is still outstanding is the origin of magnetic anisotropy. We do not yet know how the details of the electronic orbitals result in differences in magnetic properties, for instance between the soft iron in a transformer yoke and the hard magnetic materials like Nd2Fe14B that are used in motors and synchrotron undulators. Recent theories for transition metals like iron and cobalt [1] have proposed a close-to-linear relationship between the electron orbital moment, the magneto-crystalline anisotropy and the lattice distortion parameter. It might thus be said that the orbital moment links the microscopic lattice structure with the macroscopic magnetic behaviour.
X-ray Magnetic Circular Dichroism (XMCD) allows one to probe orbital moments directly, and indeed strong dependencies of the orbital magnetic moment of transition metals on the dimension of the structure (surfaces, multilayers, clusters) have been measured. Here we show the power of XMCD in a study of the orbital moment in Nd2Fe14B.
Nd2Fe14B has been characterised structurally and magnetically in a very detailed way, because of its technological importance. Specifically, it shows a Spin Reorientation Transition (SRT), in which the magnetisation, lying along the c-axis at high temperature, begins to rotate, upon cooling, below 135 K towards the [110] axis, reaching a tilting angle of ![]() = 30° at 4.2 K (see inset Figure 80). This magnetic transition is accompanied by strong magnetoelastic effects [2].
= 30° at 4.2 K (see inset Figure 80). This magnetic transition is accompanied by strong magnetoelastic effects [2].
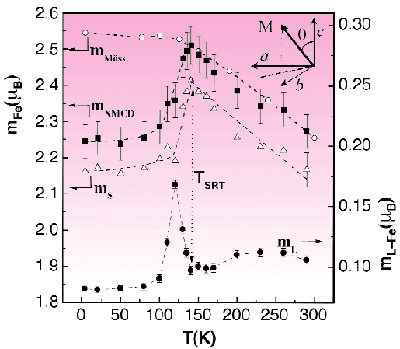 |
Fig. 80: Temperature dependence of the projected orbital-, spin- and total Fe magnetic moment compared with the modulus obtained from Mössbauer spectroscopy.
|
In our work we performed temperature dependent XMCD measurements at the Fe L2,3 edges at ID12B, on a Nd2Fe14B single crystal mounted with its c-axis parallel to the light and field directions. Application of the sum rules on the dichroic spectra yielded the c-axis projected orbital (mL), spin (mS) and total (mXXMCD = mL + mS) Fe magnetic moments (Figure 80). Above TSRT the XMCD derived total moment agrees quantitatively with that derived from Mössbauer spectroscopy. Below TSRT the ratio of the XMCD and Mössbauer moments give, in an elegant way, the average tilting angle ![]() Fe(T) of the Fe moments (Figure 81a), which has finally solved a long controversy about the low temperature magnetic structure of Nd2Fe14B.
Fe(T) of the Fe moments (Figure 81a), which has finally solved a long controversy about the low temperature magnetic structure of Nd2Fe14B.
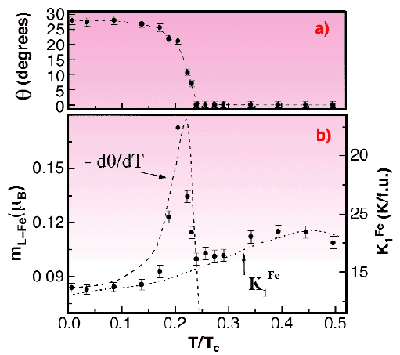 |
Fig. 81: a) Temperature dependence of the canting angle of the magnetisation; b) Fe orbital moments from Figure 80 compared with the scaled derivative of the order parameter (dashed line) and the macroscopic anisotropy of Y 2Fe 14B (dotted line), all plotted versus reduced temperature T/T c.
|
Furthermore, the most striking aspect of the data is the behaviour of the orbital moment, which shows an anomalous increase with temperature to a broad maximum at 230 K, on which a sharp peak centred around 120 K is superimposed.
In Figure 81b this curve is compared with the macroscopic anisotropy parameter of the Fe sublattice, K1Fe of the isomorphous compound Y2Fe14B (dotted line), showing convincingly the proportionality of the two data sets, except for the peak below TSRT. Since the temperature dependence of K1Fe had been correlated previously with the tetragonal lattice distortion of Nd2Fe14B, we conclude that the relationship between K1Fe, mL and the tetragonal distortion is experimentally confirmed to a good first order approximation.
The remaining question is the origin of the sharp anomaly in mL(T) below the SRT. First we note in Figure 81b that it is nearly proportional to the rate of change of the order parameter d ![]() Fe(T)/dT, which implies that it is intrinsically associated to the critical dynamics of the phase transition. Can this peak be related to the similar behaviour of K1Fe and/or a tetragonal distortion? For the former there are no data because the reference compound (Y2Fe14B) has no SRT. For the latter, magnetostriction data [2] show a clear divergence in the tetragonal distortion, also just below the SRT. Its origin remained unclear in the original work but now can be interpreted as critical behaviour.
Fe(T)/dT, which implies that it is intrinsically associated to the critical dynamics of the phase transition. Can this peak be related to the similar behaviour of K1Fe and/or a tetragonal distortion? For the former there are no data because the reference compound (Y2Fe14B) has no SRT. For the latter, magnetostriction data [2] show a clear divergence in the tetragonal distortion, also just below the SRT. Its origin remained unclear in the original work but now can be interpreted as critical behaviour.
References
[1] P. Bruno, Phys. Rev. B 39, 865 (1989); O. Hjortstam et al., Phys. Rev. B. 55, 15026 (1997).
[2] P. A. Algarabel et al., J. Magn. Magn. Mater. 84, 109 (1990).
Principal Publication and Authors
L.M. García (a), J. Chaboy (a), F. Bartolomé (a) and J.B. Goedkoop (b), Phys. Rev. Lett., 85, 429-432 (2000); J. of Appl. Phys. 87, 6567-6569 (2000).
(a) CSIC-Universidad de Zaragoza (Spain)
(b) University of Amsterdam (The Netherlands)



