- Home
- Users & Science
- Scientific Documentation
- ESRF Highlights
- ESRF Highlights 2000
- Electronic States and Lattice Dynamics
- Inhomogeneous Electron Gas: a Compton Scattering Study on Beryllium
Inhomogeneous Electron Gas: a Compton Scattering Study on Beryllium
Compton scattering experiments aim to determine the three-dimensional electron momentum density distribution of the system under study. In solids, the electrons of interest are the valence electrons, and the fundamental questions one can address are, typically, the electron-electron and the electron-ion interactions. Practically, most of the methods for calculating valence-electron wave functions in solids are based on the one-electron picture neglecting the so-called correlation effects [1,2]. In the Compton scattering theory, the correlation effects are usually taken into account by the Lam-Platzman correction (LPC) [2], which is usually considered adequate in the case of a homogeneous electron gas. The only nearly homogeneous electron gas systems in solids are the metals with one valence electron per primitive unit cell, that is the alkali metals like Li, Na, K, and Rb. In other metals the validity of the LPC has not yet been extensively studied.
We have studied the incident energy dependence of the Compton scattering cross-section and the momentum density of Be single crystals at ID15B and ID16. We measured the Compton scattering cross-section using incident photon energies of 10 (ID16), 29 and 56 keV (ID15B). The momentum space resolution in the experiments was 0.02, 0.08 and 0.16 atomic units, respectively. The measured Compton profiles are compared to an accurate local density approximation (LDA) based calculation of the momentum density in Be, the correlation effects being incorporated using the LPC.
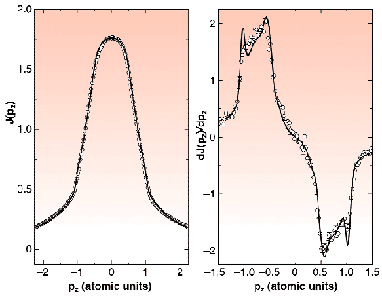 |
Fig. 71: Left panel: the measured (circles) and theoretical (solid line) Compton profiles of Be with the scattering vector along the [110] reciprocal lattice vector. Right panel: the corresponding first derivative.
|
An example of the measured and calculated Compton profiles is presented in Figure 71. The left panel shows the Compton profile taken with the scattering vector along the reciprocal lattice vector [110], and with the incident photon energy of 29 keV. The right panel shows the corresponding first derivative. Together are plotted the calculated profile and the corresponding derivative, both broadened to reflect the finite experimental resolution. The fine structure in the derivative arises directly from the complicated Fermi surface structure of Be, consisting of well-known "cigars" and "coronets". The overall agreement between the experiment and the theory is very good, although one can notice that some subtle discrepancies still exist. The sharp structures seen in the derivative of the computed profile are substantially broader in the experimental profile, more than can be explained by the experimental resolution. Figure 72 shows difference spectra obtained by subtracting the experimental Compton profiles taken with incident photon energy of 56 keV from the calculated ones where the LPC has already been taken into account. For comparison, the LPC is also plotted in the same figure. The similarity between the residual difference and the LPC clearly shows that the calculation underestimates the LPC by approximately a factor of two.
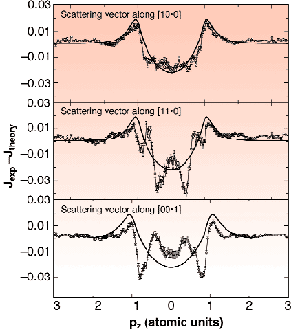 |
Fig. 72: The differences between the experimental and theoretical Compton profiles in the measured three scattering vector directions (circles), together with the utilised LPC (solid line).
|
Besides this large effect, one also notices that some sharp structures are still present in the differences. The discrepancies observed in both figures seem to indicate that the isotropic LPC is not completely adequate for a description of the correlation effects in an inhomogeneous electron gas like Be, and that a better treatment of the correlation effects is needed to account for the data.
References
[1] K. Hämäläinen, S. Huotari, J. Laukkanen, S. Manninen, C.-C. Kao, T. Buslaps and M. Mezouar, Phys. Rev. B 62, R735-R738 (2000), and references therein.
[2] L. Lam and P.M. Platzman, Phys. Rev. B 9, 5122 (1974).
Principal Publication and Authors
S. Huotari (a), K. Hämäläinen (a), S. Manninen (a), S. Kaprzyk (b), A. Bansil (b), W. Caliebe (c), T. Buslaps (d), V. Honkimäki (d) and P. Suortti (d), Phys. Rev. B 62, 7956-7963 (2000).
(a) University of Helsinki (Finland)
(b) Northeastern University, Boston (USA)
(c) Institut für Festkörperforschnung, Jülich (Germany)
(d) ESRF



