Anomalous properties of the acoustic excitations in glasses on the mesoscopic length-scale

Glasses are structurally disordered systems. As common experience shows, they support sound waves within the macroscopic limit as do the corresponding crystalline materials. In fact, when averaging on a length-scale sufficiently large, the details of the microscopic arrangement become essentially irrelevant. This holds true for sound waves with long wavelengths λ of at least several hundreds of nanometres, corresponding to wavenumbers q=2π/λ in the 10^-2 nm^-1 range, the same as those probed with light scattering techniques. On further increasing q, hence decreasing λ, the effect of the structural disorder must at one point appear. The dynamic properties of glasses for much larger q-values (a few nm^-1) are also well known, since they can be accessed experimentally with inelastic X-ray and neutron scattering techniques, and numerically with molecular dynamics simulations. These studies clearly indicate that, as in crystals, acoustic excitations with frequencies ω = cq exist up to that q range, where c is the sound velocity. However, these excitations in glasses are very broad, quite different from those in crystals whereby all atoms oscillate at the same frequency ω.  Glass exitations correspond to a complex superposition of atomic motions with different frequencies distributed around an average frequency. Unfortunately, experimental and numerical studies leave a gap in the q-range between a few nanometres and hundreds of nanometres that is extremely difficult to access. We present here molecular dynamics computer simulation results for a model glass that allow us to explore this previously inaccessible region. We find in this region new characteristic properties of the acoustic excitations that are anomalous with respect to crystals. We show that such acoustic properties are at the origin of the universal behaviour found in the specific heat of glasses in the ~10 K temperature range.

At low temperatures, the specific heat of simple dielectric crystals is dominated by the contribution of the acoustic excitations. The acoustic modes can be well described as propagating plane waves with a very simple linear relation between their frequency and their wavenumber, ω(q) = cq (dispersion relation) for a frequency range up to the sub-THz. This forms the basis of the well-known Debye or continuum model, that predicts a T³-dependence for the specific heat at low temperature and a ω²-dependence for the vibrational density of states g(ω) at low frequencies. These predictions have indeed been confirmed experimentally for simple dielectric crystals. Glasses, despite their characteristic structural disorder, also display a universal low-temperature dependence of the specific heat, and a broad excess over the Debye T³-prediction at temperatures of ~10 K and below, a region where the Debye approximation works well for the corresponding crystals [1]. This excess is related to an excess found at ~1 THz in the vibrational density of states over the Debye ω²-prediction and manifests itself as a broad bump, known as the boson peak, appearing in the reduced density of states g(ω)/ω². This implies that glasses are characterised by some sort of soft modes in excess of the acoustic ones in the THz frequency range. The physical origin of these modes has been hotly debated in the literature for many decades and an accepted solution has yet to be reached.

Classical molecular dynamics simulations provide an important tool to study the vibrational properties of glasses that is complementary to the experimental techniques of inelastic X-ray and neutron scattering. In particular, numerical simulation techniques have been used to study the acoustic excitations in the frequency range of the boson peak. The ensemble of results available to date supports a scenario where the longitudinal acoustic excitations show a linear dispersion relation and a broadening that grows quadratically with frequency with no special feature in the frequency region where the boson peak appears [2]. However, these studies could not provide a definitive answer because the largest wavelengths that could be studied - fixed by the simulation box size and then ultimately by computer power - were still in the range of few tens of interatomic spacings. As a consequence, the corresponding lowest frequency acoustic excitations that were accessible lay too close to the boson peak position to allow definite conclusions in this supposedly crucial frequency range.

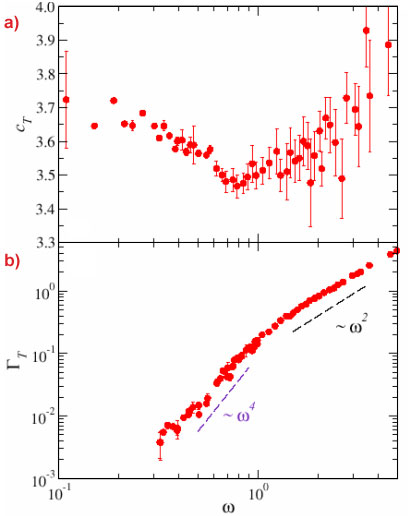
We report here on a study of the vibrational dynamics of a monatomic glass model using the classical Lennard-Jones (LJ) interatomic potential. Specifically, we present results for exceptionally large simulation boxes containing up to ~10⁷ particles and gain insight into the acoustic modes in the frequency region where the boson peak appears. Figure 1a shows sound velocity data corresponding to transverse polarisation. The data show an increase with frequency (positive dispersion) for ω > 0.8 as already reported for the longitudinal sound velocity in the same glass [2]. It is interesting to observe that below this frequency the macroscopic (ω → 0) sound velocity limit is not directly recovered: this manifests itself in the region where the velocity increases with decreasing frequency, which is exactly the region where the boson peak is found in this LJ glass (ω ~ 2). The boson peak does not appears in a frequency range where the acoustic excitations disperse linearly (constant phase velocity), but rather where they experience a more complex dispersion behaviour. This is important because it implies that the Debye continuum approximation for the acoustic excitations breaks down at frequencies comparable to the boson peak position [3], i.e. at frequencies much lower than previously expected. Complementary information on this issue can be found in Figure 1b, where the corresponding frequency dependence of the acoustic excitations broadening, Γ_T, is presented. Γ_T is directly related to the acoustic attenuation. These data clearly show two different regimes for the acoustic attenuation: a ω²-regime at high frequencies, as already known from previous studies and associated to the structural disorder of the glass [2], and a previously unnoticed ω⁴-regime at low frequencies. The frequency that marks the change of regime is again close to the boson peak position. Starting from these observations, we managed to infer a quantitative connection, showing that the boson peak originates from these newly discovered anomalies in the acoustic properties.

Figure 1. Frequency dependence of sound velocity (a) and attenuation (b) of the transverse acoustic excitations of an LJ glass.  The low frequency region is characterised by glass-specific anomalies: on increasing frequency, the sound velocity decreases and the acoustic attenuation strongly increases. These features help us to understand the universal thermal anomalies found in glasses at low temperature.

Summing up, we have shown that in glasses the elastic continuum approximation for the acoustic excitations breaks down abruptly on the mesoscopic, medium-range-order length scale of about ten interatomic spacings, where it still works well for the corresponding crystalline systems. This breakdown is signalled by a reduction of the sound velocity and increase of the acoustic attenuation, which turns out to be closely related to the aforementioned anomalies in the specific heat and vibrational density of states and finally can be traced back to the elastic properties specific to glasses.

References
[1] W.A. Phillips, Amorphous Solids: Low Temperature Properties (Springer, Berlin, 1981).
[2] G. Ruocco et al., Phys. Rev. Lett. 84, 5788 (2000).
[3] G. Monaco and V.M. Giordano, Proc. Natl. Acad. Sci. USA 106, 3659 (2009).
[4] The image has been produced with V_Sim, a visualisation tool by D. Caliste (http://www-drfmc.cea.fr/sp2m/L_Sim/V_Sim/index.en.html).

Principal publication and authors
G. Monaco (a), S. Mossa (b,a), Anomalous properties of the acoustic excitations in glasses on the mesoscopic length-scale, Proc. Natl. Acad. Sci. USA 106, 16907 (2009).
(a) ESRF
(b) CEA, Grenoble (France)

Top image: Local displacement field corresponding to a sound wave propagating in a glass. The cubic simulation box was cut along a vertical plane to emphasise the details of the 3-D structure; Colours indicate local field direction [4].