- Home
- Users & Science
- Scientific Documentation
- ESRF Highlights
- ESRF Highlights 2014
- Dynamics and extreme conditions
- Role of disorder in the thermodynamics and atomic dynamics of glasses
Role of disorder in the thermodynamics and atomic dynamics of glasses
In the late 1950s, the low-temperature thermal conductivity of glasses was found to be several orders of magnitude smaller and the heat capacity several times bigger [1] than those of crystals. The anomalously low thermal conductivity was soon successfully explained by phonon scattering caused by disorder. However, the understanding of the excess of the heat capacity demanded longer studies.
The excess of the heat capacity in glasses at ~10 K was found to be associated with a similar excess of the vibrational excitations in the ~1 THz frequency range of the density of states (DOS) g(E) [2]. In the reduced DOS presentation, g(E)/E2, these states form a distinct peak (the so-called ‘boson’ peak) at a position where the reduced DOS of the corresponding crystals is nearly flat. This excess of heat capacity and the corresponding excess of vibrational states are universally observed for all glasses and with all relevant experimental techniques. Nevertheless, the results of numerous studies still do not converge to a unified answer on how disorder causes these features. Recent experiments conducted at beamlines ID18 and ID28 have now revealed that disorder actually is not responsible.
The studies were performed on SiO2, which exists in various glassy and crystalline polymorphs with different structures and densities. The density (ρ) of the most common SiO2 glass (ambient silica glass, ρ = 2.20 g / cm3) is smaller than the density of the most common crystal (α-quartz, ρ = 2.65 g/cm3). However, SiO2 also exists in a lower density crystalline form (α-cristobalite, ρ = 2.29 g/cm3). The density of this crystal is nearly the same as the density of the ambient glass. Furthermore, SiO2 exists also in a higher-density glassy form (densified silica glass, ρ = 2.67 g/cm3). The density of this glass is nearly the same as the density of α-quartz. Thus, SiO2 offers a suitable 2×2 matrix of (dis)order versus density, which allows for a model-independent evaluation of the relative role played by structural disorder and density.
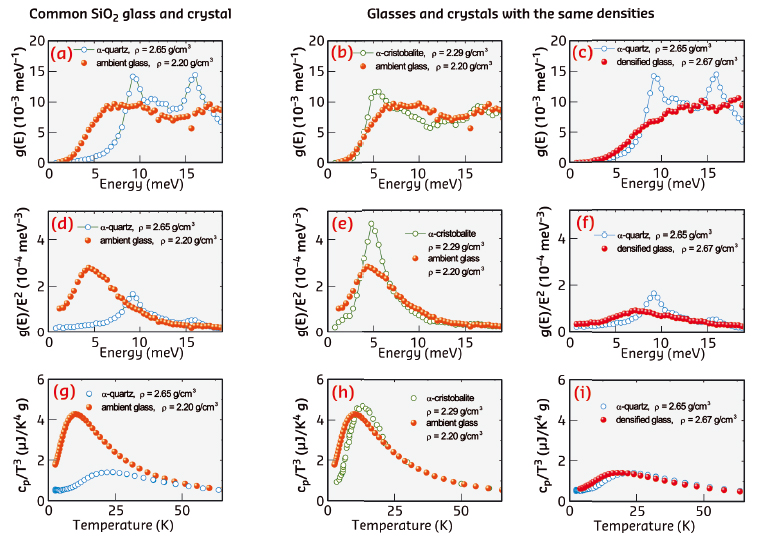
The measured DOSs revealed that SiO2 glasses have the same number of low-energy states and the same number of excess states as SiO2 crystals. For the most common glass, these states are located at lower energy than for the typical crystal and provide the higher heat capacity (left column of Figure 74).
 |
|
Fig. 74: The density of states g(E) (a–c), the reduced density of states g(E)/E2 (d–f), and the heat capacity cP/T3 (g–i) for various glassy and crystalline polymorphs of SiO2. The left panels (a, d, g) compare the most common glassy and crystalline polymorphs and reveal a noticeable difference in the displayed properties. The middle and the right panels compare the glassy and crystalline polymorphs with matched densities, namely, the low-density (b, e, h) and high-density (c, f, i) polymorphs. They demonstrate that the atomic dynamics and thermodynamics of the glassy and crystalline polymorphs with matched densities do not differ much from each other. From Ref. [3]. |
For glasses and crystals with matched densities (middle and right columns of Figure 74), the excess states are located in the same energy region and provide the same heat capacity. Furthermore, the boson peak of glasses appears as a smooth counterpart of the van Hove acoustic singularity of the corresponding crystals.
Thus, being responsible for the anomalous thermal conductivity of glasses, disorder does not greatly affect the frequency spectrum of the atomic vibrations and the heat capacity. The usually lower heat capacity of glasses is caused by their usually lower density.
Principal publication and authors
A.I. Chumakov (a), G. Monaco (b, a), A. Fontana (b, c), A. Bosak (a), R.P. Hermann (d, e), D. Bessas (d, e, a), B. Wehinger (a), W.A. Crichton (a), M. Krisch (a), R. Rüffer (a), G. Baldi (f), G. Carini Jr. (g), G. Carini (h), G. D’Angelo (h), E. Gilioli (f), G. Tripodo (h), M. Zanatta (i, c), B. Winkler (j), V. Milman (k), K. Refson (l), M. T. Dove (m), N. Dubrovinskaia (n), L. Dubrovinsky (n), R. Keding (o) and Y.Z. Yue (p), Physical Review Letters 112, 025502 (2014).
(a) ESRF
(b) University of Trento (Italy)
(c) University of Rome (Italy)
(d) Jülich Centre for Neutron Science and Peter Grünberg Institut (Germany)
(e) University of Liege (Belgium)
(f) IMEM-CNR, Parma (Italy)
(g) IPCF-CNR, Messina (Italy)
(h) University of Messina (Italy)
(i) University of Perugia (Italy)
(j) Goethe-University, Frankfurt (Germany)
(k) Accelrys, Cambridge (UK)
(l) STFC Rutherford Appleton Laboratory, (UK)
(m) Queen Mary University of London (UK)
(n) University of Bayreuth (Germany)
(o) Max Planck Institute for the Science of Light, Erlangen (Germany)
(p) Aalborg University (Denmark)
References
[1] R.C. Zeller, R.O. Pohl, Phys. Rev. B 4, 2029 (1971).
[2] U. Buchenau, N. Nücker and A.J. Dianoux, Phys. Rev. Lett. 53, 2316 (1984).
[3] A.I. Chumakov and G. Monaco, J. Non-Cryst. Solids 407, 126-132 (2015).



