- Home
- Users & Science
- Scientific Documentation
- ESRF Highlights
- ESRF Highlights 2012
- Dynamics and extreme conditions
- Femtosecond movies of confined water reconstructed from IXS data
Femtosecond movies of confined water reconstructed from IXS data
An understanding of nanoconfined water and structure water has been a fundamental challenge to physics and chemistry and has important consequences in molecular biology and environmental sciences. Recent experimental and computational results have given interesting but conflicting results, ranging from liquid-like water to solid-like water.
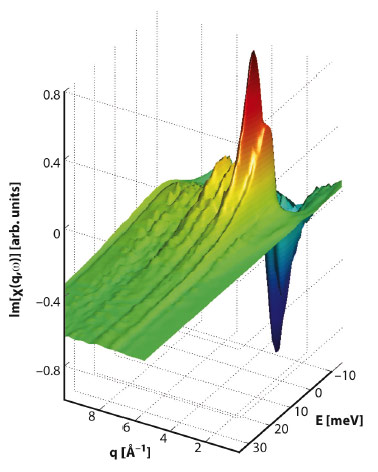
The dynamical structure factor S(q,ω) measured by inelastic X-ray scattering (IXS) contains detailed information regarding the interactions of a system. This can be seen in the dispersion relations directly derived from IXS measurements, but it can also be seen in other ways. The electrodynamical response function χ(q,ω) can be extracted from measurements of χ(q,ω) by Kramers-Kronig relations. Recently, we showed that the portion of χ(q,ω) that encapsulates the solvent response on molecular time and length scales in liquid water can be extracted from meV-IXS measurements of χ(q,ω) performed at beamline ID28 [1] (Figure 51). The Fourier-transformed real space Green’s function χ(r-r’,t-t’) can be used to image density fluctuations to resolutions of roughly 20 fs in time and 0.4 Å in space.
 |
|
Fig. 51: The imaginary part of χ(q,ω), as determined by applying the Fluctuation-Dissipation theorem to the measured dynamic structure factor S(q,ω): Im[χ(q,ω)]=- π[S(q,ω)- S(q,-ω)]. |
Using this measured response function we examined how a ‘bulk’ homogeneous fluid responds to nanoconfinement. In doing so, we distinguish confinement effects from the termination of a bulk fluid from effects that originate in confinement-induced phase transitions. We computationally reconstructed the dynamical hydration structure of water between two hydrophilic sheets, modelled as semi-infinite slabs separated by a distance D and decorated with charge dipole interaction sites [2]. Here, we show the dynamics of a confined water layer when one slab is sheared while the other remains stationary.
We found a variety of distinct hydration structures that changed both with the degree of confinement and the dipole density on each surface. For large D, the hydration structure in between the sheets is essentially bulk-like, and the influence of one sheet on the other is imperceptible. Even at roughly 1 nm away from the surface, the density fluctuations are still indistinguishable from bulk-like water. As the intermolecular bond length between molecules is only about 0.3 nm, only a few layers of water interact with the surface.
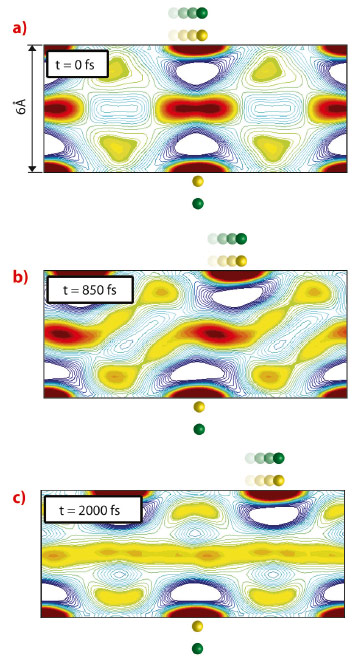
Of particular interest is the nanoconfined water dynamics observed as the hydrophilic slabs are sheared past one another. When D approaches 10 Å, these few layers of water decorating each sheet begin to interact more strongly with one another. However, water remains bulk-like between the two distorted surface-associated hydration layers. When D decreases to 6 Å (nominally two water molecular thicknesses), the two surface-associated hydration layers are forced to reconstruct into a single, frustrated layer. A series of “freeze-melt” behaviour is observed in this layer of water: As one hydrophilic slab shears past the other, this layer transforms from a well-defined layer bridging the two surfaces, called “freeze” (Figure 52a), to completely amorphous, delocalised layer, “melt” (Figure 52c), as the dipoles across the gap become out of register. Interestingly, as the dipole density increases, the hydration structures between nearest neighbour dipole sites on the same slab begin to interfere, creating a continuous hydration structure on that slab. In this limit, the “freeze-melt” dynamics disappear as the slabs are sheared.
 |
|
Fig. 52: The shear dynamics of water confined between hydrophilic slabs separated by D = 6 Å and decorated by dipoles (green/yellow spheres) with inter-dipole distance a = 7 Å. In this reconstruction, the top slab is being sheared with a velocity of 200 m/s past the stationary bottom slab. Red and blue contours indicate regions of water density that are respectively greater than or less than bulk. When the shearing dipoles are in register with the stationary ones (a), the water density is localised, bridging the static hydration shells of the nearest dipole sites on each slab, as if they were “frozen”. As the top slab becomes out of register with the bottom, this structure transforms (b) and begins to become amorphous. When the slabs are completely out of register (c), the layer between them “melts” into a disordered, one-dimensional fluid layer. The process is reversed as the sites come back into register, leading to periodic “freeze-thaw” dynamics. |
These results have interesting implications. We found that a broad range of observations from our system agree with other experimental and computational studies of confined water, and may reconcile disparate results on confined water – this is surprising since we started with bulk response functions. That the “freeze-melt” behaviour is seen to essentially disappear may have implications for high lubricity surfaces, such as those found in biology (ex: the highly charged and disordered polymer brushes found in mamalian joints). We hope to apply our hybrid technique to reconstructing water dynamics in other interesting geometries.
Principal publication and authors
R.H. Coridan (a), N.W. Schmidt (a), G.H. Lai (a), P. Abbamonte (b) and G.C.L. Wong (a), Physical Review E 85, 031501 (2012).
(a) University of California, Los Angeles (USA)
(b) University of Illinois at Urbana-Champaign (USA)
References
[1] R.H. Coridan, N.W. Schmidt, G.H. Lai, R. Godewat, M. Krisch, S. Garde, P. Abbamonte and G.C.L. Wong, Physical Review Letters 103, 237402 (2009).
[2] R.H. Coridan, N.W. Schmidt, G.H. Lai and G.C.L. Wong, Journal of Physics: Condensed Matter 21, 424115 (2009).



