- Home
- Users & Science
- Scientific Documentation
- ESRF Highlights
- ESRF Highlights 2011
- Soft condensed matter
- Dynamics of concentrated colloidal suspensions revisited
Dynamics of concentrated colloidal suspensions revisited
Suspensions of colloidal particles are valuable experimental model systems for exploring phase behaviour and dynamics in condensed matter. Hard-sphere-like colloidal particles can form colloidal crystals or colloidal glasses at volume fractions above Φf = 0.494 or Φg~0.57, respectively, allowing the investigation of the dynamics of the freezing and glass transitions.
Colloidal particles are much bigger and slower than atoms, thus the metastable state can be studied in real-time using the well-established technique of dynamic light scattering (DLS), or the more recently developed technique of X-ray photon correlation spectroscopy (XPCS). The fundamental quantity accessible via both DLS and XPCS is the intermediate scattering function (ISF), f(q,![]() ), which describes the dynamics (or time evolution) of particle number density, where q is the scattering vector and
), which describes the dynamics (or time evolution) of particle number density, where q is the scattering vector and ![]() is the delay time.
is the delay time.
For concentrated suspensions, the dynamics are often divided into three regimes: a short-time regime, where particles diffuse within their neighbour cages; a non-diffusive crossover regime or plateau, where the interactions between a particle and its neighbours are most clearly exposed; and a long-time diffusion regime where the particles have escaped their neighbour cages. The short- and long-time diffusion coefficients, Ds(q) and DL(q), are usually used to quantify these processes [1]. The long-time regime is difficult to access experimentally, and ambiguities in interpretation can arise depending on the method of data analysis.
Using DLS, Segré & Pusey [1] measured the short- and long-time diffusion coefficients of sterically-stabilised hard spheres and found that the ratio Ds(q)/DL(q) is independent of q, exposing a scaling of the dynamics. However, Lurio et al. [2] did not observe this scaling when applying XPCS to charge-stabilised pseudo-hard spheres. Possible explanations for this discrepancy are: (i) there is a fundamental difference between XPCS and DLS; (ii) X-ray damage contributes to the results using XPCS; (iii) the charge-stabilised pseudo-hard sphere system is not equivalent to the steric-hard-sphere; and/or (iv) different analysis methods lead to ambiguities in interpretation.
To elucidate this discrepancy, we directly compared XPCS (at ID10A) and DLS (at RMIT) on colloidal suspensions of hard-sphere particles, thus eliminating sample preparation as a variable. We conducted analyses similar to those in [1, 2], and compared the results.
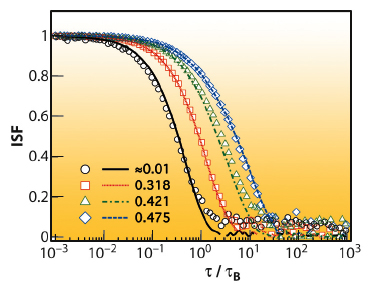
Figure 70 shows the ISFs obtained from XPCS and DLS for several volume fractions Φ. Good sample statistics are harder to obtain with XPCS but very good agreement is observed, demonstrating the equivalence of the techniques.
 |
|
Fig. 70: ISF from XPCS (symbols) and DLS (lines) at qR = 3.48 and Φ values indicated. |
We also investigated the scaling of the dynamics by calculating the time-dependent quantity, D(q,![]() ), from the numerical derivative of the ISF [1]. This quantity describes the evolution from short- to long-time processes. The observation of plateaux in D(q,
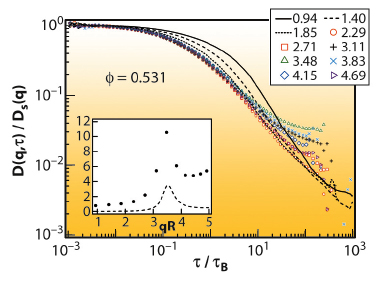
), from the numerical derivative of the ISF [1]. This quantity describes the evolution from short- to long-time processes. The observation of plateaux in D(q,![]() ) allows the identification of diffusive regimes at short- and long-times characterised by Ds(q) and DL(q). Figure 71 shows D(q,t)/Ds(q), for several scattering vectors at Φ = 0.531.
) allows the identification of diffusive regimes at short- and long-times characterised by Ds(q) and DL(q). Figure 71 shows D(q,t)/Ds(q), for several scattering vectors at Φ = 0.531.
 |
|
Fig. 71: D(q, |
The coincidence of the curves at low delay time in Figure 71 confirms the short-time scaling behaviour found by Segré & Pusey [1]. The short-time diffusion regimes exist at all volume fractions and scattering vectors, and Ds(q) scales with the structure factor S(q) (see inset Figure 71). However in the long-time regime there is significant q-dependence, and long-time diffusive regimes are only observed near the peak of the structure factor at high volume fractions.
Thus the existence of a collective long-time diffusive regime is rather questionable. The constant ratio Ds(q)/DL(q) observed by Segré & Pusey [1], but not by Lurio et al. [2], is not observed. We argue that the absence of a long-time diffusive regime is due to the fact that particles are unable to move sufficiently far for number density fluctuations, at least for scattering vectors away from the main maximum in the static structure factor, to forget packing constraint effects during accessible time scales.
As far as we are aware, this work forms the first comprehensive comparison between DLS and XPCS on concentrated colloidal samples. We found that the two techniques are equivalent, but that DLS provides better statistics. However, DLS is only possible for suspensions that are carefully refractive-index matched to minimise multiple scattering (like ours). As most concentrated suspensions have significant multiple scattering, XPCS would be the ideal choice for many samples.
Principal publication and authors
V.A. Martinez (a,b), J.H.J. Thijssen (a), F. Zontone (b), W. van Megen (c) and G. Bryant (c), J. Chem. Phys. 134, 054505 (2011).
(a) School of Physics and Astronomy, The University of Edinburgh (UK)
(b) ESRF
(c) Applied Physics, School of Applied Sciences, RMIT University (Australia)
References
[1] P.N. Segre and P.N. Pusey, Phys. Rev. Lett. 77, 771 (1996).
[2] L.B. Lurio, et al., Phys. Rev. Lett. 84, 785 (2000).



