Resonant inelastic X-ray scattering (RIXS) is a powerful spectroscopic tool for examining both ground state and excited state electronic structure of complex materials. In the RIXS process a high-energy incoming photon excites a deep core electron, creating a photoelectron, and an outgoing photon is radiated when the empty core state is filled. We have recently developed a theoretical description of the direct RIXS process based on a real-space Green’s function approach within a real-space multiple scattering (RSMS) framework. Due to the importance of many-body effects on RIXS spectra, ab initio calculations can be quite demanding. With several simplifying assumptions, however, we find that RIXS can be approximated as a convolution of the X-ray absorption (XAS) and X-ray emission spectra (XES). Additional many-body effects can be taken into account via a convolution with a spectral function. In particular, we find that the Kramers-Heisenberg equation,


can be approximated by

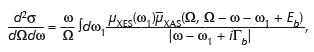
where Ω is the frequency of the incoming photon, ω is the frequency of the outgoing photon, Eb is the deep core-level energy, and Γb is the inverse core-hole lifetime, and unless otherwise noted, we have used atomic units, e = = m = 1. As in the RSMS treatment of XAS [2], the effective X-ray absorption signal µXAS can also be

expressed in terms of Green’s functions, where T(ω) is a non-local, energy dependent operator that replaces the usual dipole operator in XAS, and gc (ω + Ec) is the single particle Green’s function calculated in the presence of a core hole in level |c>i and shifted by the core energy Ec. With this expression, we obtain a theoretical description of RIXS that includes core hole effects in both the intermediate and final states of the system. If we neglect core-hole effects µXAS is equivalent to the usual XAS, yielding the simpler result

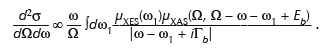
This formula is similar to one involving a convolution of occupied and unoccupied densities of states [1], except that it now builds in transition-matrix elements. Additional many-body effects can be included a posteriori via convolution of this expression with a many-body spectral function A(ω,ω’). This approach has been implemented as an extension to the FEFF9 RSMS code, which has been used extensively for various spectroscopies [2,3]. The RSMS formalism in FEFF is advantageous since it does not rely on any particular symmetry, making it possible to treat periodic and aperiodic systems alike, including molecules and amorphous systems, over a broad spectral range. As an illustration, our implementation has been used to investigate core-hole effects on the RIXS of anatase TiO2.

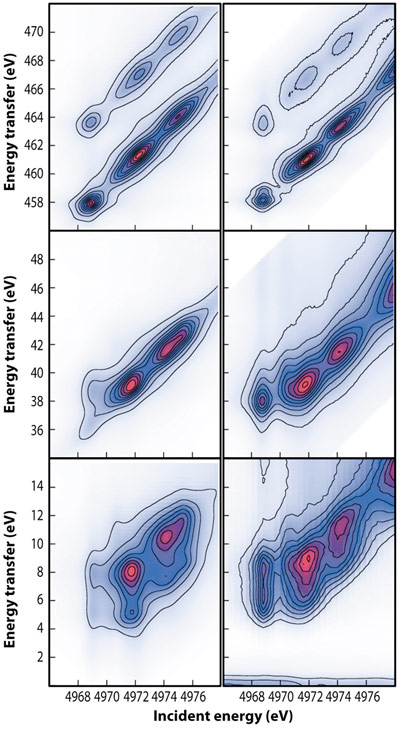
Fig. 26: Calculated (left) and experimental (right) RIXS spectra of TiO2 as a function of incident and transferred energies. The Ti K-α, -β, and –valence spectra are shown from top to bottom.

Figure 26 shows the calculated Ti K-α, -β, and –valence spectra of TiO2 as a function of incident photon-energy Ω, and energy transfer Ω – ω compared to experiment. Overall, the experimental results (left) are reproduced fairly well by the calculations (right). In addition, the calculations reproduce the qualitative behaviour as a function of the core-hole depth. The core hole potential is strongest in the 1s intermediate state of the X-ray absorption process and gives rise to a K absorption pre-edge feature that extends over 8 eV [4]. The core hole potential is weaker in the final state with a vacancy in the 2p (K-α), 3p (K-β) or valence shell. This can be directly observed in the RIXS planes: The first peak progresses to higher energy transfer as the final state core-hole becomes shallower, going from a final state with a 2p core hole (top) to a final state with a 3p core hole (middle), then to a final state with a valence hole (bottom). We thus observe that states localised around the absorbing atom in TiO2 anatase - which are strongly affected by the core hole - migrate toward higher energy transfer as a function of the strength of the core hole. We conclude that the key interactions in hard X-ray RIXS can now be satisfactorily modelled in terms of XAS and XES using an RSMS formalism, thus opening the way toward a more quantitative interpretation.

 

Principal publication and authors

J.J. Kas (a), J.J. Rehr (a), J.A. Soininen (b) and P. Glatzel (c), Phys. Rev. B 83, 235114 (2011).

(a) Department of Physics, University of Washington, Seattle (USA)

(b) Department of Physics, University of Helsinki (Finland)

(c) ESRF

 

References

[1] P. Glatzel et al., J. Am. Chem. Soc. 132, 2555 (2010).

[2] J.J. Rehr et al., Comptes Rendus Physique 10, 548 (2009).

[3] J.J. Rehr and R.C. Albers, Rev. Mod. Phys. 72, 621 (2000).

[4] D. Cabaret et al., J. Synchrotron Radiat. 6, 258-260 (1999).

 

Acknowledgement

This research was supported by DOE BES Grant DE-FG03-97ER45623, the DOE CMCSN (JJR,JJK), the Eemil Aaltonen and Magnus Ehrnrooth Foundations (JAS) and by the ESRF (PG).