The thermal conductivity of amorphous materials is many orders of magnitude smaller than that of the corresponding crystalline structures and presents a peculiar plateau at temperatures of a few Kelvin [1]. The existence of this plateau requires the mean free path of propagating phonon-like excitations to decrease at least with the fourth power of frequency. This strong scattering regime is usually referred to as Rayleigh scattering, after the pioneering work of Lord Rayleigh [2]. In the same temperature range (T ~ 1-10 K) where the thermal conductivity shows the characteristic plateau, the specific heat of glasses, C(T), is marked by an excess over the normal T3 behaviour, which appears as a maximum in C(T)/T3. This maximum is associated with an excess of vibrational modes over the ∝ ν2 Debye density of states at frequencies of a few terahertz; it is known as the boson peak. Substantially different theories of wave propagation in disordered media predict the presence of Rayleigh scattering in glasses in the frequency range below the boson peak position. Discriminating among the various theoretical models, however, is difficult since experimental access to the relevant frequency range is very challenging.

In addition to Rayleigh scattering, the sound waves in glasses can be attenuated by a variety of other attenuation mechanisms, all associated with some degree of anharmonicity. These mechanisms give rise to a complex frequency and temperature dependence of the sound attenuation and controversial results have been reported [3,4]. Exploiting the intense development of the inelastic X-ray scattering (IXS) technique during the last decade, we have obtained clear evidence that in vitreous silica this strong scattering regime is located in the few terahertz frequency range. We show as well that the Rayleigh scattering persists up to a crossover frequency which coincides with the position of the boson peak, confirming a clear connection between the damping of the acoustic-like excitations and the excess of vibrational modes.

The experiment was performed at beamline ID16. IXS spectra were collected at several values of the scattering angle (different exchanged wavevectors). Each spectrum presents an elastic line and a Brillouin doublet corresponding to the longitudinal acoustic excitation. A suprasil fused-quartz sample was heated to a very high temperature, T=1620 K, to enhance the inelastic signal over the elastic one. At this temperature the boson peak position is 50% higher in frequency with respect to room temperature, allowing us to measure the longitudinal excitations with IXS at frequencies below the boson peak position in silica glass for the first time.

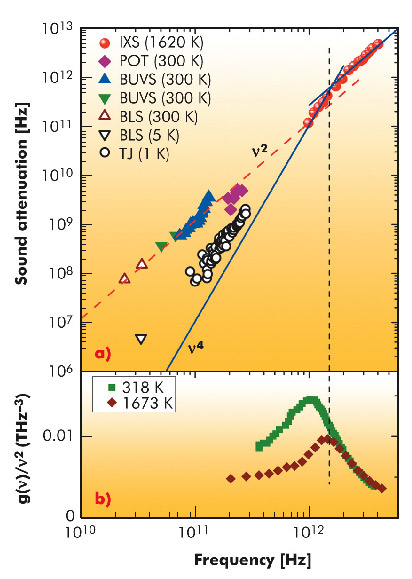
Fig. 8: a) Sound attenuation of vitreous SiO2 as a function of frequency in log-log scale. The points at high frequency (red circles) are from the new IXS data at T=1620 K. Lower frequency data are from the literature: picosecond optical technique (POT), Brillouin ultraviolet scattering (BUVS), Brillouin light scattering (BLS) and a tunneling junction (TJ) technique. The dashed line (red) is a quadratic frequency slope. The blue lines are two power law fits, ~n2 and ~n4, to the IXS data. b) Reduced density of vibrational states from literature data, at the indicated temperatures. The vertical dashed line indicates the boson peak position at the temperature of the IXS experiment.

The sound attenuation coefficient obtained with IXS is plotted as a function of frequency in the upper panel of Figure 8, together with the values measured by lower frequency probes. The comparison between the data at room temperature and at a few Kelvin shows that the mean free path is temperature dependent up to 300 GHz and thus affected by anharmonic processes. In this frequency range the damping at room temperature follows an almost quadratic frequency dependence which extrapolates to the first point of the new IXS data. Here the disorder induced term, Rayleigh scattering, dominates the anharmonic/relaxational contributions. The sound attenuation is then proportional to the fourth power of frequency up to a crossover point, which coincides with the boson peak position at the investigated temperature (see the vertical dashed line in Figure 8).

In summary, the new IXS data give clear evidence of a Rayleigh scattering regime in glasses. This observation represents the first direct measurement of the Rayleigh law up to the boson peak frequency in vitreous silica, confirming the theoretical prediction of the existence in glasses of this peculiar attenuation mechanism.

 

Principal publication and authors

G. Baldi (a), V.M. Giordano (b), G. Monaco (b) and B. Ruta (b), Phys. Rev. Lett. 104, 195501 (2010).
(a) IPCF-CNR, UOS ROMA, c/o Physics Department, University of Parma (Italy)
(b) ESRF

References

[1] W.A. Phillips, Amorphous Solids: Low Temperature Properties (Springer, Berlin, 1981).
[2] J.W.S. Rayleigh, The Theory of Sound (The Macmillan Company, 1896) Vol. II.
[3] C. Masciovecchio et al., Phys. Rev. Lett. 97, 035501 (2006).
[4] A. Devos et al., Phys. Rev. B 77, 100201(R) (2008).