- Home
- Users & Science
- Scientific Documentation
- ESRF Highlights
- ESRF Highlights 2011
- Electronic structure and magnetism
- Violation of Hund’s third rule in structurally-disordered ferromagnets
Violation of Hund’s third rule in structurally-disordered ferromagnets
Hund’s rules were formulated for atomic physics and refer to the coupling of the spin and orbital moments of atoms. These rules have also been shown to generally hold for solid magnetic materials, alloys and molecules. In the past decade a number of experimental works report on the violation of Hund’s third rule, which is observed for metallic multilayers (Fe/W) [1] and for bulk ErCo2 in a narrow temperature range [2]. Theoretical calculations have been suggesting a dependence of the observation of the break down of Hund’s third rule and the structure and chemical environment.
Amorphous materials present an interesting playground to test such ideas, as the atomic arrangement differs vastly from their crystalline counterparts. In this work, we probed the induced spin and orbital moment of Zr in amorphous Fe- and Co- based alloys with XMCD and compared them to crystalline alloys. The experimental data and a theoretical analysis prove that by altering the coordination number and bond length, a violation of Hund’s third rule can be obtained.
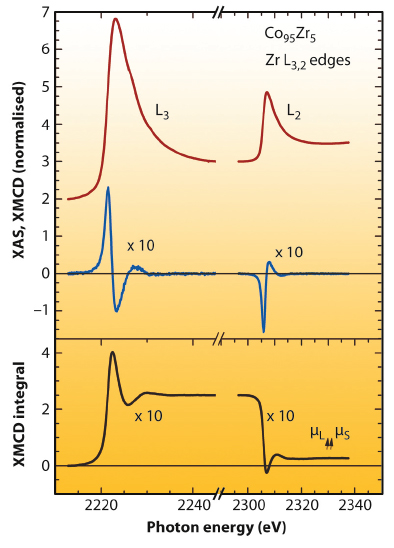
Figure 79 presents normalised XANES spectra of amorphous Co95Zr5 for the L2.3 edges of Zr, at the temperature of 300 K. The data were recorded at the ID12 beamline using the total fluorescence yield detection mode in a backscattering geometry. A clear and sizeable XMCD signal for Zr was detected, revealing an induced magnetic moment for Zr. Knowing the direction of the magnetic field and the helicity of the beam we were able to determine the alignment of the Zr moment with respect to Co or Fe. In all cases the Zr moment was aligned antiparallel to the Co or Fe magnetic moment.
Application of the sum rule analysis on the XAS and XMCD results allows the determination of the spin and orbital contributions to the magnetic moment of Zr. Only for the case of amorphous Fe91Zr9 or Co95Zr5, the spin and orbital magnetic moments for Zr are found to be parallel, as can also be seen in the lower part of Figure 79.
 |
|
Fig. 79: XANES and XMCD spectra at the L2.3 edges of Zr in amorphous Co95Zr5. The XMCD integral in the lower part of the figure reveals a parallel alignment of the spin and orbital magnetic moment. |
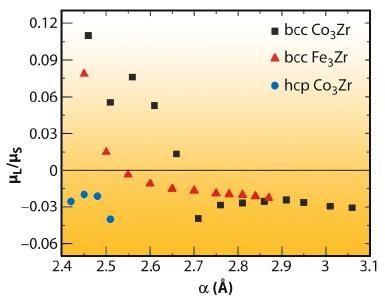
First-principles calculations were performed in order to elucidate this effect. The results, which are summarised in Figure 80, clearly indicate a sign reversal of the orbital magnetic moment occurs as the interatomic distance between Co(Fe) and Zr decreases. Recent experimental results have demonstrated the reduction of the interatomic distances between dissimilar atoms and chemical short-range order in amorphous alloys [3,4].
 |
|
Fig. 80: First-principles calculation of the induced orbital and spin magnetic moment ratio for Zr, as a function of the lattice parameter and for various crystallographic structures. |
In summary, a violation of Hunds´s third rule is observed as a consequence of changes in the local atomic structure. These changes can be obtained in amorphous materials, in which both the electron and atomic structure can be adjusted through the composition of the material. Further experimental and theoretical efforts are needed to enhance our understanding of the complex and unique properties of amorphous materials.
Principal publication and authors
V. Kapaklis (a), P.T. Korelis (a), B. Hjörvarsson (a), A. Vlachos (b), I. Galanakis (b), P. Poulopoulos (b), K. Özdogan (c), M. Angelakeris (d), F. Wilhelm (e) and A. Rogalev (e), Physical Review B 84, 0244411 (2011).
(a) Uppsala University (Sweden)
(b) University of Patras (Greece)
(c) Yildiz Technical University (Turkey)
(d) Aristotle University of Thessaloniki (Greece)
(e) ESRF
References
[1] F. Wilhelm, P. Poulopoulos, H. Wende, A. Schertz, K. Baberschke, M. Angelakeris, N. K. Flevaris and A. Rogalev, Phys. Rev. Lett. 87, 207202 (2001).
[2] J. Herrero-Albillos, L. M. García, F. Bartolomé, A. T. Young, Europhys. Lett. 93, 17006 (2011).
[3] X. Liu, X.D. Hui, H.Y. Hou, T. Liu and G.L. Chen, Phys. Lett. A 372, 3313 (2008).
[4] A. Hirata, P. Gua, T. Fujita, Y. Hirotsu, A. Inoue, A.R. Yavari, T. Sakurai and M. Chen, Nat. Mater. 10, 28 (2011).



