- Home
- Users & Science
- Scientific Documentation
- ESRF Highlights
- ESRF Highlights 2011
- Dynamics and extreme conditions
- Lattice dynamics of cerium metal across the gamma to alpha transition
Lattice dynamics of cerium metal across the gamma to alpha transition
Many physical and chemical properties of the light rare-earths and actinide elements are governed by an active role of f electrons, at the border between localisation and itinerancy. This is reflected in very rich phase diagrams and anomalous pressure and temperature dependence of many physical quantities. However, despite intensive efforts, the detailed mechanisms of phase stability and phase transitions remain poorly understood.
Undoubtedly the most famous example is the isostructural γ–α transition in cerium which was discovered more than seven decades ago and remains the only known solid-solid transition in an element that has a phase boundary ending at a critical point. At ambient temperature, the first order transition occurs at 7.5 kbar, and leads to a volume decrease of the fcc lattice by ~15% [1].
New insights into this intriguing phase transition were recently gained through an inelastic X-ray scattering experiment conducted at beamline ID28 on a single crystal of cerium metal compressed up to P = 25 kbar at T = 297 K, in conjunction with ab initio lattice dynamics calculations.
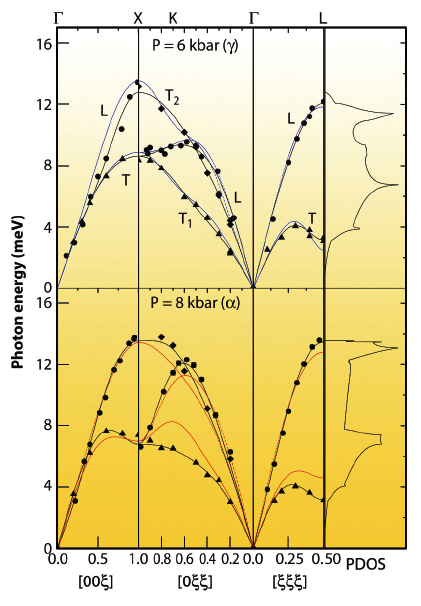 |
|
Fig. 12: Phonon dispersion of cerium metal at 6 kbar (g-phase) and 8 kbar (a-phase). L branches (circles), T1<110> branch (diamonds), and T2<001> branches (triangles). The black solid lines are the results of a Born von-Kármán fit. The corresponding phonon density of states (PDOS) is reported in the right panels. The blue and red lines represent ab initio calculations (within GGA, and using the PBE parameterisation) with the trivalent potential and tetravalent potential, respectively, both scaled by 0.9. |
The experimental phonon dispersions just below (P = 6 kbar) and above (P = 8 kbar) the transition are reported in Figure 12, together with a Born-von Kàrmàn force constant model fit and the results of the ab initio calculations. We note that several of the phonon branches show significant changes; the most striking one occurs for the longitudinal acoustic (LA) branch along the [110] direction. A quantitative representation of the phonon energy changes, E, across the transition is provided by the mode Grüneisen parameters,
![]()
displayed in Figure 13. While positive values of γq (increase of phonon energy with increasing pressure/decreasing volume, V) are common behaviour, negative values can occur as precursor of phase transitions or as a signature of electron-phonon interactions. Besides the low-q portion of the L[001] branch and a small portion of the T[111] branch around q = 0.3, the most pronounced regions of negative γq’s occur around the X point. It is interesting to note that the suggested ordering of electrical quadrupoles in the α-phase, though never directly observed, leads to strong coupling to the phonons at the X point [2].
The vibrational entropy change per atom across the transition can be derived directly from the corresponding phonon density-of-states (PDOS) using well established integral equations, and we obtain ∆Svibγ-α of 0.33 ± 0.03 kb, in remarkable agreement with ultrasound measurements performed 50 years ago [3], thus underlining that the lattice contribution to the phase transition cannot be neglected.
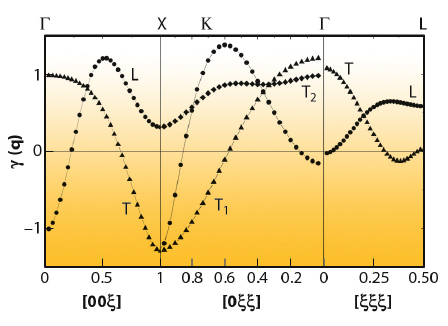 |
|
Fig. 13: Evolution of the mode Grüneisen parameters across the γ -> α transition in cerium as derived from the Born von-Kármán fit to the experimental dispersion. |
Ab initio calculations of the γ-phase, treating the 4f electron as localised (trivalent potential), yield the best agreement with experiment, while in the α-phase best agreement is achieved when the 4f electron is treated as part of the valence band (tetravalent potential). Our experimental results provide a unique benchmark to test theoretical models and will stimulate further experimental efforts to improve our understanding of this unique isostructural phase transformation.
Principal publication and authors
M. Krisch (a), D.L. Farber (b), R. Xu (c), D. Antonangeli (b,d), C.M. Aracne (b), A. Beraud (a), T.-C. Chiang (c), J. Zarestky (e), D. Y. Kim (f), E. Isaev (f), R. Ahuja (f) and B. Johansson (f,g), PNAS 108, 9342-9345 (2011).
(a) ESRF
(b) Lawrence Livermore National Laboratory, Livermore, California (USA)
(c) Department of Physics, University of Illinois at Urbana-Champaign (USA) and Frederick Seitz Materials Research Laboratory, Urbana, Illinois (USA)
(d) Institut de Minéralogie et Physique des Milieux Condensés, UMR CNRS 7590, Institut de Physique du Globe de Paris, Université Pierre et Marie Curie, Université Paris Diderot (France)
(e) Ames Laboratory and Department of Physics and Astronomy, Iowa Sate University, Ames, Iowa (USA)
(f) Condensed Matter Theory Group, Physics Department, Uppsala University (Sweden)
(g) Department of Materials and Engineering, Applied Materials Physics, Royal Institute of Technology, Stockholm (Sweden)
References
[1] P.W. Bridgman, Proc. Am. Acad. Arts Sci. 62, 207 (1927).
[2] A.V. Nikolaev and K.H. Michel, Eur. Phys. J. B 9, 619 (1999); 17, 363 (2000).
[3] F.F. Voronov, L.F. Vereshchagin and V.A. Goncharova, Soviet Physics-Doklady 135, 1280 (1960).



