- Home
- Users & Science
- Scientific Documentation
- ESRF Highlights
- ESRF Highlights 2008
- High resolution and resonance scattering
- Playing billiards with electrons: double photoionisation with a single photon
Playing billiards with electrons: double photoionisation with a single photon
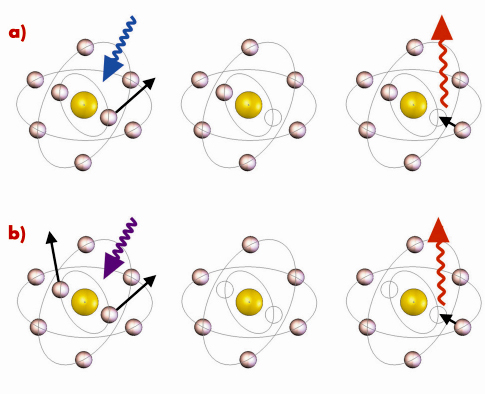
A single photon can directly ionise only one electron of an atom. A simultaneous ejection of a second electron, i.e. double photoionisation, may occur only if the electrons within the atom interact with each other. If both electrons are ejected from the K-shell, a so-called hollow atom is formed, wherein the K shell is empty while higher shells are populated (Figure 5). Hollow atoms are of a great interest in many fields, ranging from atomic physics to surface science. When decaying by a 1s2 ![]() 1s12p1 transition (underlining denotes hole states) they emit a Kh
1s12p1 transition (underlining denotes hole states) they emit a Kh![]() 1,2 hypersatellite photon [1]. Thus, double photoionisation and electron-electron interactions can be studied by high-resolution X-ray hypersatellite spectra measurements.
1,2 hypersatellite photon [1]. Thus, double photoionisation and electron-electron interactions can be studied by high-resolution X-ray hypersatellite spectra measurements.
 |
|
Fig. 5: Schematic representation of the processes for a) single photoionisation and b) double photoionisation, where wavy arrows denote photons, and straight arrows, electron motions. The final state of the hypersatellite emission process is left with a spectator hole, which is later filled by another electron creating conventional diagram X-ray emission lines. |
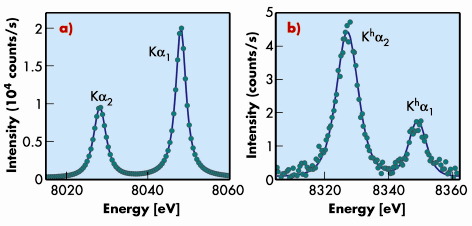
Using beamlines ID16 (ESRF) and X25 (NSLS, USA) we have studied double photoionisation near its energy threshold, Eth, in 3d transition metals, by high-energy-resolution hypersatellite spectroscopy. Figure 6 compares the conventional Cu K![]() 1,2 diagram spectrum of a 1s1
1,2 diagram spectrum of a 1s1 ![]() 2p1 transition with its hypersatellite counterpart. The I(K
2p1 transition with its hypersatellite counterpart. The I(K![]() 1)/I(K
1)/I(K![]() 2) = 2 intensity ratio reflects the number ratio of the LIII and LII electrons. For hypersatellites, the measured ratio is vastly different, being determined by selection rules rather than by the LIII/LII electron number ratio. The Kh
2) = 2 intensity ratio reflects the number ratio of the LIII and LII electrons. For hypersatellites, the measured ratio is vastly different, being determined by selection rules rather than by the LIII/LII electron number ratio. The Kh![]() 1 line requires flipping the shell-changing 2p electron’s spin, which is forbidden in the LS coupling dominating low-Z atoms. In the range of Z studied here such flipping is partly allowed, and the Kh
1 line requires flipping the shell-changing 2p electron’s spin, which is forbidden in the LS coupling dominating low-Z atoms. In the range of Z studied here such flipping is partly allowed, and the Kh![]() 1 line has a non-zero intensity.
1 line has a non-zero intensity.
 |
|
Fig. 6: a) The conventional Cu K |
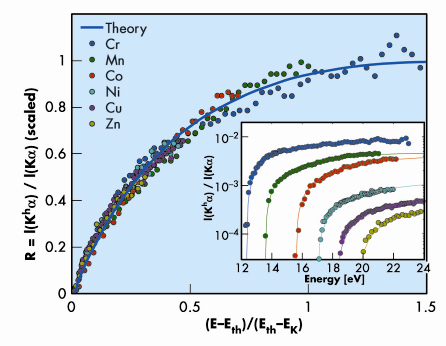
Figure 7 (inset) shows measured R=I(Kh![]() 1,2)/I(K
1,2)/I(K![]() 1,2) intensity ratios vs. ionising photon energy. This is the first systematic measurement of the near-threshold behaviour of R for a range of elements. The very long saturation range, ~70% of Eth, stands out immediately. Eth and the saturation ranges and values in the inset differ among the elements. Nevertheless, when scaled by the binding energies of the indirectly-ionised K-electrons and the saturation values (which, incidentally, are found to decrease as ~Z–1.6) an intriguing universal behaviour is revealed: all curves collapse onto a single curve (Figure 7).
1,2) intensity ratios vs. ionising photon energy. This is the first systematic measurement of the near-threshold behaviour of R for a range of elements. The very long saturation range, ~70% of Eth, stands out immediately. Eth and the saturation ranges and values in the inset differ among the elements. Nevertheless, when scaled by the binding energies of the indirectly-ionised K-electrons and the saturation values (which, incidentally, are found to decrease as ~Z–1.6) an intriguing universal behaviour is revealed: all curves collapse onto a single curve (Figure 7).
 |
|
Fig. 7: Relative double photoionisation probability R for various elements as a function of the excess photon energy above threshold, E-Eth, scaled by the binding energy of the secondary ionised electron, Eth-EK, where EK is the binding energy of the directly-ionised primary electron. The inset shows the raw cross-sections for each element. The solid curve is the (scaled) theoretical KO prediction [2]. |
How does the double photoionisation occur? For photons of energies E >> Eth, the ionised electron is ejected with a very high kinetic energy, changing abruptly the atomic potential acting on the other electrons. The secondary electron finds itself in an excited state, and has a finite probability of being ejected. This is the shake-off (SO) model, which, however, is invalid close to Eth, where the ionising photon’s energy is just barely enough to overcome the binding energy of the electron. Of the other theoretical models only the knock-out (KO) model [2] agrees well (blue line in Figure 7 and lines in the inset) with the measured universal evolution of R near threshold, where the ejected photoelectron is slow and stays longer within the bounds of the atom. In the KO model the double photoionisation proceeds by the directly-ionised electron knocking out the secondary one, as in billiards, on its way out. Moreover, the KO process turns out to be a quasi-classical, rather than a quantum, effect, in spite of its occurrence within the sanctum sanctorum of the quantum regime: the inner bounds of the atom. Thus, double photoionisation seems to evolve from a quasi-classical KO billiards process near threshold to a fully quantum SO effect at high ionising photon energies.
In conclusion, we have determined double photoionisation probabilities by measuring the evolution of the hypersatellite spectrum from the threshold upwards for elements 23 ![]() Z
Z ![]() 30. We suggest that near the threshold the excitation is a quasi-classical KO effect rather than a quantum mechanical SO one, and demonstrate a universal scaling law for the double photoionisation energy evolution near threshold.
30. We suggest that near the threshold the excitation is a quasi-classical KO effect rather than a quantum mechanical SO one, and demonstrate a universal scaling law for the double photoionisation energy evolution near threshold.
Principal publication and authors
S. Huotari (a), K. Hämäläinen (b), R. Diamant (c), R. Sharon (c), C.C. Kao (d), and M. Deutsch (c), Phys. Rev. Lett. 101, 043001 (2008).
(a) ESRF
(b) Division of Materials Physics, Department of Physics, University of Helsinki (Finland)
(c) Physics Department, Bar-Ilan University (Israel)
(d) National Synchrotron Light Source, Brookhaven National Laboratory (USA)
References
[1] R. Diamant, S. Huotari, K. Hämäläinen, R. Sharon, C.C. Kao, and M. Deutsch, Phys. Rev. Lett. 91, 193001 (2003).
[2] T. Schneider and J.M. Rost, Phys. Rev. A 67, 062704 (2003).



