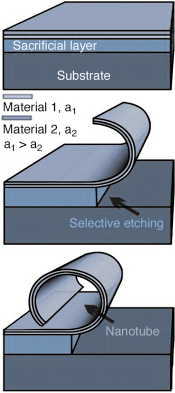
Crystals with cylindrical symmetry, which do not exist in nature, are mimicked by the roll-up of single crystalline and highly pseudomorphically strained GaAs/InGaAs semiconductor bilayers. The resulting objects, the rolled-up nanotubes (RUNTs) [1], are depicted in Figure 80.

Fig. 80: Formation principle of the rolled-up nanotubes.

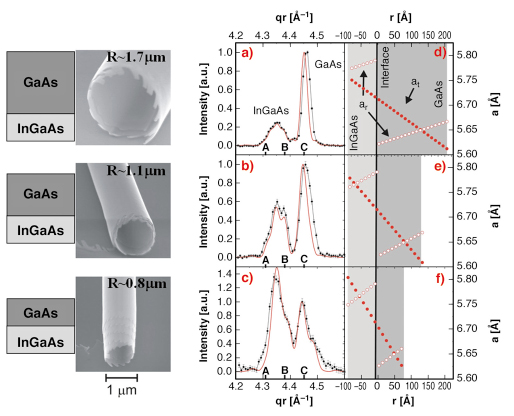
We established a method to find and measure individual single nanotubes coherently connected with the substrate. Their structure was probed and quantified non-destructively by X-ray microbeam diffraction. Varying the composition and thicknesses of the layers allows tailoring of the tube formation and properties. As an example, results for three different layer thicknesses (thus yielding different tube diameter) are shown in Figure 81 (left).

Fig. 81: (left) Schematic view of the bilayer and SEM images of the resulting nanotubes (R is the tube diameter); (a-c) Intensity distribution, normalised to the GaAs (004) reflection. The experimental data are shown as black dots, the simulations as red lines. (d-f) simulation results of the data before: lattice parameter distribution in tangential direction (at, filled symbols) and in radial direction (ar, open symbols) as function of the distance r from the interface (r = 0) between the GaAs and InGaAs layers in the bilayer.

For all samples measured, the crystalline bilayer is still present in the RUNTs as proved by the observation of two well-separated Bragg peaks: one peak close to the bulk GaAs position (marked as C in Figure 81 (a-c)); and another between the strained InGaAs position A, found in the as-grown film perpendicular to the substrate, and the completely relaxed position B, i.e. the InGaAs lattice parameter expected from Vegard’s law. This intermediate position of the InGaAs peak shows that the individual layers only partially relax since both of them exert strain on each other.

With increasing GaAs layer thickness, the intensity ratio between the GaAs and the InGaAs peak increases. The shape of the peaks is determined by the interference of the X-rays scattered by both layers. From the comparison to simulations based on the minimisation of the elastic energy, we determined in a non-destructive way the layer thicknesses, the lattice parameter distribution (both along the tangential direction, at and along the radial direction, ar) and strain within the rolled-up single crystalline bilayer. The continuum elasticity theory proved to be applicable even for layers as thin as 10 nm and allows us to understand their formation in full agreement with the experimental data (for more details see the publication).

Such objects show a great potential as integrative components, including 2D confined channels for fluid filling and transport, coils, transformers, capacitors, or (optical) wave guides [2].

 

References

[1] V.Y. Prinz et al., Physica (Amsterdam) 6E, 828 (2000); O.G. Schmidt, K. Eberl, Nature (London) 410, 168 (2001).
[2] C. Deneke, O.G. Schmidt, Appl. Phys. Lett. 85, 2914 (2004); O.G. Schmidt et al., IEEE J. Sel. Top. Quantum Electron. 8, 1025 (2002); S. Mendach et al., Appl. Phys. Lett. 88, 111120 (2006).

Principal Publication and Authors

B. Krause (a,*), C. Mocuta (a), T.H. Metzger (a), Ch. Deneke (b) and O.G. Schmidt (b), Phys. Rev. Lett. 96, 165502 (2006).
(a) ESRF
(b) Max-Planck-Institut fuer Festkoerperforschung, Stuttgart (Germany)
(*) now at Carl Zeiss GmbH (Germany)