- Home
- Users & Science
- Scientific Documentation
- ESRF Highlights
- ESRF Highlights 2000
- Materials
- Time-resolved Study of Grain Growth in Nanocrystalline Fe
Time-resolved Study of Grain Growth in Nanocrystalline Fe
Understanding the influence of the grain size on the kinetics of grain growth is essential to the technological application of nanocrystalline materials, in which the average grain size is several orders of magnitude smaller than in conventional samples. According to the theory of grain growth at conventional grain sizes, the rate at which a grain boundary moves depends only on the boundary curvature, leading to a parabolic dependence of the grain size on the annealing time. However, when a specimen's grain size lies in the nanometre range, another process might replace curvature-induced migration as the rate-controlling step for grain growth. Indeed, a recent publication by Estrin, Gottstein and Shvindlerman [1] predicts that the redistribution of the excess volume localised in the grain-boundary cores imposes an upper bound on the growth rate when the grains are smaller than a critical size, causing the grains to grow linearly with time. As the critical size is crossed, the growth kinetics should change smoothly from linear to parabolic, and the activation energy for boundary migration should drop by a factor of 2 (as a result of the change in the rate-controlling mechanism).
We have attempted to test these predictions by measuring the kinetics of grain growth in a nanocrystalline Fe sample prepared by ball milling. The grain size of a nanocrystalline material can be characterised by wide-angle X-ray diffraction through a Fourier analysis of the size-broadened Bragg peak profiles. The latter procedure is successful only when good counting statistics can be achieved under measurement conditions yielding minimal instrumental distortion of the peak profiles. These requirements are fulfilled by the high-resolution powder diffractometer at BM16, where measurement times as short as two minutes sufficed for determining the average grain size and strain level in nanocrystalline Fe through a Warren-Averbach analysis of the (110)/(220) peak pair. Using a hot-air blower, we were able to heat the samples (sealed in quartz capillaries) to constant temperatures as high as 1000°C. In this manner, we could perform isothermal studies of the grain-size evolution over a wide range of temperatures with unprecedented time resolution a prerequisite for detecting the predicted change from linear to parabolic kinetics at the critical grain size.
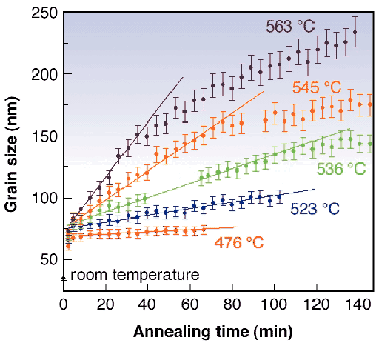 |
Fig. 96: Isothermal evolution of grain size in nanocrystalline Fe at the indicated temperatures. The straight lines illustrate the nearly linear growth at grain sizes below approximately 150 nm.
|
The initial growth behavior in nanocrystalline Fe is plotted at several temperatures in Figure 96. Following a mysterious jump in the grain size as the sample temperature equilibrated, the grains grow linearly with time, as predicted in Ref. [1], and above about 150 nm the growth curves develop a nonlinearity reminiscent of the parabolic growth found in conventional samples.
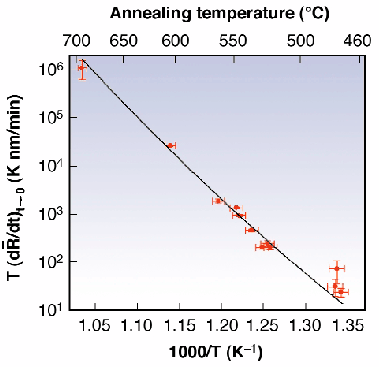 |
Fig. 97: Arrhenius plot of the initial growth rate, d
|
Figure 97 is an Arrhenius plot of the growth rate in the linear regime along with the prediction of the excess-volume-redistribution model. The surprisingly good agreement between theory and experiment indicates that the rate-controlling step for grain growth in Fe at sizes below 150 nm is the redistribution of excess volume via the transient incorporation of vacancies in the growing grains; correspondingly, the activation energy for boundary migration is that of vacancy diffusion rather than atomic diffusion within and across the grain boundaries. This finding may provide an explanation for the unexpectedly sluggish grain growth frequently observed in nanocrystalline samples and important clues for improving the thermal stability of such materials.
Reference
[1] Y. Estrin, G. Gottstein and L.S. Shvindlerman, Scripta Mater. 41, 385 (1999).
Principal Publication and Authors
C. E. Krill III (a), L. Helfen (a,b), D. Michels (a), H. Natter (a), A. Fitch (b), O. Masson (b,c) and R. Birringer (a), Phys. Rev. Lett. 86, 842-845 (2001).
(a) Universität des Saarlandes, Saarbrücken (Germany)
(b) ESRF
(c) Now at: Université de Limoges (France)



