- Home
- Users & Science
- Scientific Documentation
- ESRF Highlights
- ESRF Highlights 2000
- Magnetism
- Magnetic Domains Investigated by Coherent X-ray Scattering
Magnetic Domains Investigated by Coherent X-ray Scattering
Coherent X-ray scattering is a fast developing technique with inherent imaging and time-structured information on disordered materials. It evolved from the laser-related field to the hard X-ray range when highly collimated and intense third generation synchrotron sources became available. A disordered material may be viewed as a distribution of coherently scattering volumes introducing random phase-shifts that result in a strongly modulated diffraction or "speckle" pattern, when illuminated by a coherent incident radiation. Each pattern is uniquely related to the instantaneous spatial distribution of the disorder. If this spatial arrangement changes with time, the corresponding speckle pattern also changes. Information on the dynamics of the disordered system can thus be retrieved from the time correlation analysis of a single speckle, while the spatial information is contained in the inverse Fourier transform of the diffraction pattern. This coherent scattering technique with hard X-rays has proven successful mainly in the field of soft condensed matter [1] by giving access to a higher q-range than dynamic light scattering, and to phenomena slower than neutron scattering. However, condensed matter problems have also been successfully addressed in the 8 keV energy range, where a high flux of coherent X-rays can "easily" be obtained [2].
The study of antiferromagnetic domains is a new and exciting area of application for such a combination of imaging and dynamic techniques. Domain formation is inherent to most types of magnetic ordering because of crystal symmetry. However, to date little is known about the size of the domains and their arrangement in antiferromagnetic materials. The extreme weakness of the magnetic scattering signal makes it a challenging experiment. UAs was chosen as a test system for which advantage can be taken from the huge enhancement of the magnetic intensity through a resonant process at the MIV uranium absorption edge (3.728 keV).
In a preliminary experiment, we observed for the first time a static speckle pattern from magnetic domains in the type-I antiferromagnetic phase of UAs, at T = 100 K. UAs crystallises in the cubic NaCl structure. At TN ~ 123 K the system undergoes a first order phase transition to a magnetically ordered phase.
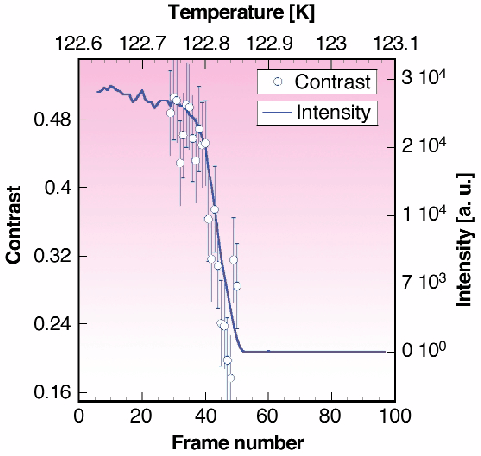 |
Fig. 77: The apparent coherence (contrast) and intensity of the magnetic (001) reflection through the magnetic transition. The contrast is a measure of the modulation of the average static diffraction pattern, and is zero for an incoherent beam and/or for a time or space averaged system.
|
In a recent experiment at beamline ID20, the speckle patterns of both the (001) magnetic and the (002) charge reflections were followed throughout the magnetic transition while varying the temperature. The evolution of both the integrated intensity and the mean apparent coherence (or contrast) of the magnetic speckle pattern is shown in Figure 77. The data were recorded with a CCD camera as a series of acquisition frames while continuously varying the temperature. Within 0.1 Kelvin the intensity drops and reaches the background value. The apparent coherence decreases at the same time indicating that the domain configuration (disorder) evolves on a time scale shorter than the measuring time, and hence smears out the speckle pattern (Figure 78). An average magnetic domain size of ~ 4 µm could be retrieved from the inverse width of the diffraction spot. Moreover, the reproducibility of the speckle pattern, while using a procedure cycling through the magnetic transition, indicates that a similar domain configuration is established each time and that the magnetic domains are probably pinned by crystal defects.
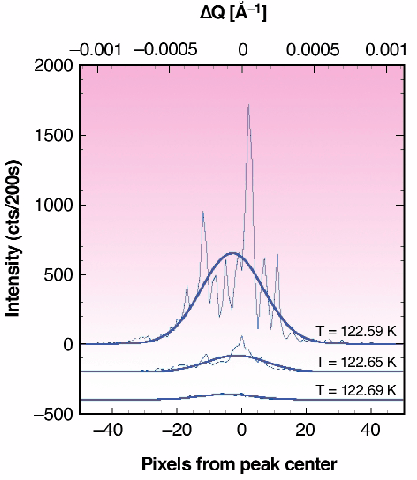 |
Fig. 78: Horizontal cuts through the 2-D magnetic speckle pattern at temperatures below and above the transition temperature. The speckles appear smeared out by a time-averaging of the fluctuating magnetic domain configuration.
|
These promising results strongly suggest that this is the first observation of magnetic domain fluctuations at a first order phase transition. Real space imaging through the inverse Fourier transform of the 2-D diffraction pattern remains to be done. However, the feasibility of coherent scattering experiments on magnetic systems at large diffraction angles has been established and this opens the way to new exciting fields of investigation.
References
[1] G. Grübel, D.L. Abernathy, D.O. Riese, W.L. Vos and G.H. Wegdam, J. Appl. Cryst. 33, 424 (2000).
[2] S. Brauer, G.B. Stephenson, M. Sutton, R. Brüning, E. Dufresne, S.G.J. Mochrie, G. Grübel, J. Als-Nielsen and D.L. Abernathy, Phys. Rev. Lett. 74, 2010 (1995); F. Bley, F. Livet, J.C. Leroux, J-P. Simon, D.L. Abernathy, J. Als-Nielsen, G. Grübel, G. Vignaud, G. Dolino, J-F. Legrand, D. Camel, N. Menguy and M. Papoular, Acta Cryst. A51, 746 (1995).
Principal Publication and Authors
F. Yakhou (a), A. Létoublon (b), F. Livet (b), M. de Boissieu (b), F. Bley (b) and C. Vettier (a), to be published in Journal of Magnetism and Magnetic Materials.
(a) ESRF
(b) LTPCM-ENSEEG, St Martin d'Hères (France)



