- Home
- Users & Science
- Scientific Documentation
- ESRF Highlights
- ESRF Highlights 2000
- Electronic States and Lattice Dynamics
- Sound Velocities in Iron to Megabar Pressures
Sound Velocities in Iron to Megabar Pressures
Physical properties of iron are of interest to a better understanding of both the current state of planetary cores and their formation during the differentiation of planets. The knowledge of the elastic constants and wave velocities of the different phases of iron, which makes up 70-90 wt% of planetary cores, is essential for comparison with global seismic models of the Earth. Among the different structures, the hexagonal closed-packed (hcp or e) high-pressure phase of iron might be the stable phase at the pressure of 360 GPa at the Earth's centre. However, to date, direct measurements of sound wave velocities have been limited in iron to an ultrasonic study to 16.5 GPa and to Hugoniot dynamic shock wave measurements [1]. At the ESRF, inelastic X-ray scattering (IXS) with meV energy resolution has recently been shown to be a technique suited to study the pressure dependence of phonon dispersion curves [2].
IXS experiments were carried out at high-pressure on iron at the inelastic-scattering beamline ID28. The undulator X-ray beam was monochromatised by a cryogenically cooled silicon (111) crystal and by a very-high-energy resolution monochromator. This beam, with an energy of 15.618 keV and an energy resolution of 3.9 meV, was focused with a gold-coated mirror at the sample location. The scattered photons were collected by 5 spherical silicon crystal analysers operating in backscattering and Rowland circle geometry at the same reflection order as the high-resolution monochromator.
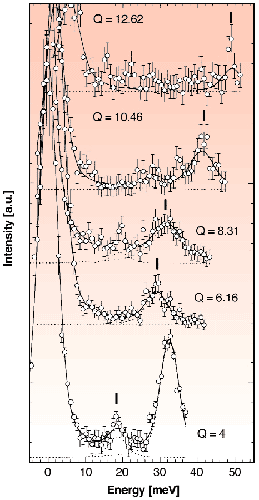 |
Fig. 61: Typical inelastic X-ray scattering spectra and corresponding fits as a function of transfer energy, at a pressure of 28 GPa. The peak centred at zero energy transfer corresponds to the elastic contribution to the signal, whereas peaks visible at higher Q values (Q in nm -1) correspond to the longitudinal acoustic (LA) phonon excitation from iron (ticks). The intense excitation observed at high energy at Q = 4 nm -1 corresponds to the transverse acoustic phonon branch of the diamond anvil cell. Integration time for each point was of the order of 600-700 s, obtained by summation of 4 to 6 scans in the range 0-50 meV. The energy position of phonons could be determined with a relative error of typically 3%.
|
The dispersion of longitudinal acoustic phonons have been measured from 19 to 110 gigapascals at momentum transfers Q varying from 4 to 12 nm-1 on polycrystalline iron compressed in a diamond-anvil cell (Figure 61). These experiments represent the first measurements of the Longitudinal Acoustic phonon branch of hcp iron at high pressures, from which acoustic velocities can be directly derived. The observed increase of the phonon frequencies corresponds to an increase of the longitudinal wave velocity (VP) from 7000 to 8800 ms-1. These results are very important to geophysics. Plotted along with shock measurements, we show (Figure 62) that hcp iron follows Birch's law for VP, namely a linear dependence between velocity and density regardless of the particular values of pressure and temperature, which provides a convenient relationship for extrapolating our measurements to the pressures of the Earth's inner core. Seismic data [3] do not fit the experimental extrapolation, suggesting that the Earth's inner core is 4 to 5 % lighter than hcp iron. This confirms initial predictions that light elements, which are thought to be present in the Earth's core to account for the excess of density of pure hcp iron when compared to seismic data [3], may thus be present not only in the liquid outer core but in the inner core as well [4], unless another iron phase with higher sound velocities is stable at the pressure and temperature conditions of the Earth's inner core.
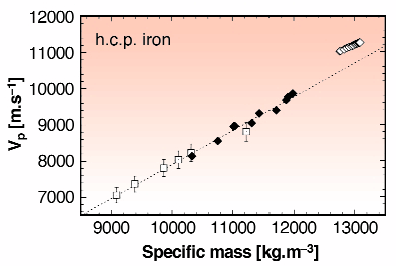 |
Fig. 62: Longitudinal acoustic wave velocities of h.c.p. iron (open squares, this work) and solid diamonds (shock-wave measurements [1]) as a function of specific mass. Preliminary Reference Earth Model seismic data are represented by open diamonds [3]. As shown by the dashed line, the experimental points for hcp iron show a linear correlation between velocity and density, according to Birch's law, regardless of ambient temperature (this work) or high temperature measurements (Hugoniot data).
|
References
[1] J.M. Brown and R.G. McQueen, J. Geophys. Res. 91, B7, 7485-7494 (1986).
[2] M.H. Krisch, A. Mermet, A. San Miguel, F. Sette, C. Masciovecchio, G. Ruocco and R. Verbeni, Phys. Rev. B 56, 14, 8691-8694 (1997).
[3] A.M. Dziewonski and D.L. Anderson, Phys. Earth Planet. Int. 25, 297-356 (1981).
[4] A.P. Jephcoat and P. Olson, Nature 325, 332 (1987).
Principal Publication and Authors
G. Fiquet (a), J. Badro (a), F. Guyot (a), H. Requardt (b) and M. Krisch (b), Science, accepted for publication.
(a) UMR CNRS 7590, Paris (France)
(b) ESRF



