The discovery of high temperature superconductivity in the fluorine doped pnictide compound LaFeAsO1-xFx, with a Tc = 26 K has reinforced the idea that the electronic correlations pairing mechanism for superconductivity in iron-based pnictides is mediated by antiferromagnetic spin fluctuations. This was suggested by the discovery of a strong increase of Tc by replacing lanthanum with magnetic rare-earth (R) elements, and SmFeAsO1-xFx reached the highest superconducting transition temperature Tc~55 K [1]. However, conflicting experimental reports have opened an intense debate about the role of magnetic coupling between the Fe and the magnetic R ions in the enhancement of the superconducting transition temperature [2,3]. Elucidating the nature and strength of this interaction between the two magnetic sublattices in the non-superconducting parent compound is an important endeavour in understanding the interplay between magnetism and superconductivity in the RFeAsO family.

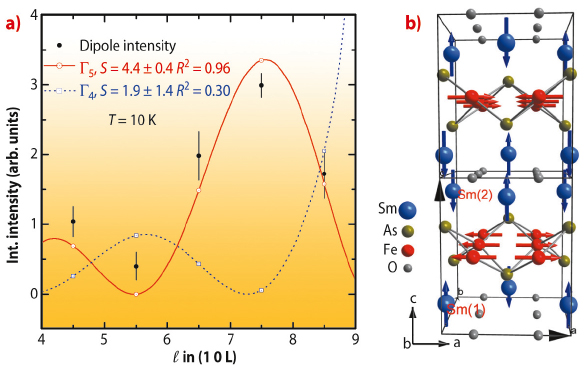
We have used element-specific X-ray resonant magnetic scattering (XRMS) and nonresonant X-ray magnetic scattering (NRXMS) to disentangle the two magnetic moment sublattice contributions in the parent compound SmFeAsO, and to investigate in detail their orientation within the unit cell. The experiments were performed at beamline ID20 for the Sm L2, L3 and Fe K absorption edges and at beamline P09 of PETRA III for the Fe K edge. Below T = 110 K, both Sm and Fe magnetic moments order with a magnetic propagation vector (1 0 1/2), as observed by the enhancement of XRMS intensities at Sm L2.3 and Fe K edges, respectively. By exploiting the peculiar polarisation dependence and site selectivity of XRMS we have determined the magnetic structure of the Sm, by collecting integrated intensities of a series of magnetic reflections measured at the Sm L2-edge, as shown in Figure 75a. Similarly, the magnetic structure of Fe sublattice was determined in the temperature range 5 K ≤ T ≤ 110 K and the final magnetic structure is shown in Figure 75b.

Fig. 75: a) l dependence of the integrated intensity at the Sm L2 edge along with the fits for the (1 0 l/2) reflections. Open symbols are the calculated intensities. Lines serve as guides to the eye. b) Proposed magnetic structure of SmFeAsO determined in the temperature range 5 K ≤ T ≤ 110 K.

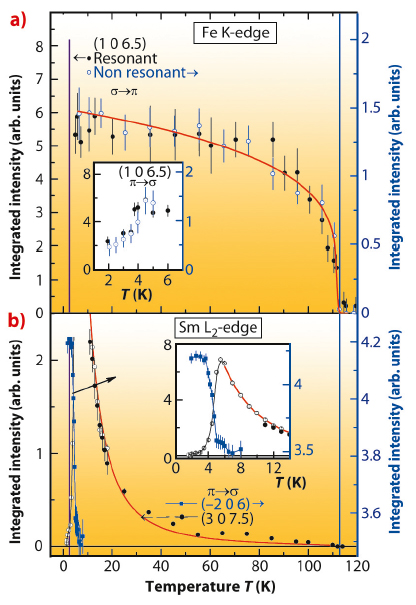
The temperature dependence of the two magnetic sublattices is represented in Figure 76, where the Fe shows a typical magnetisation curve and Sm follows a quite unusual behaviour, with a sharp increase of the intensity below 50 K, followed by a second magnetic phase transition at 5 K. This unusual temperature dependence of the Sm sublattice can be explained with a ground-state doublet crystal-field level, split by an exchange field, and can be modelled by taking into account only the ground-state doublet and a splitting [∆ (T)] proportional to the effective field [Beff(T)] produced by the Fe sublattice (see Figure 76b, red line). We obtained Beff (T = 0) = (56.4 ± 1.9) Tesla characterising the strength of interaction between the two sublattices, which is comparable or even higher than the value for Ce-Fe interaction in CeFeAsO, indicating a strong coupling between these two sublattices. Below 5 K a magnetic phase transition arises on both the sublattices, as deduced by a drop of the Fe XRMS intensity (inset of Figure 76a) and the switch of the XRMS intensities at Sm L2 edge from (3 0 7.5) reflection to the charge (−2 0 6) reflection, signalling a change in the magnetic order of Sm with the magnetic unit cell equal to the chemical unit cell.

Fig. 76: a) Temperature dependence of the (1 0 6.5) reflection measured in both resonant and nonresonant conditions near Fe K edge in polarisation channel σ-π. The inset shows the change of Fe magnetic order below 5 K in π-σ channel. b) Temperature dependencies of the (3 0 7.5) and (−2 0 6) reflections measured in resonant condition at the Sm L2 edge. The inset shows the Sm phase transition below 5K.

Our finding reveals that the magnetism of Sm and Fe in the SmFeAsO compound are strongly correlated, and shed light on the currently debated importance of the R-Fe interaction in the family of iron-based superconductors.

 

Principal publication and authors

S. Nandi (a), Y. Su (b), Y. Xiao (a), S. Price (a), X.F. Wang (c), X.H. Chen (c), J. Herrero-Martín (d), C. Mazzoli (d), H.C. Walker (d), L. Paolasini (d), S. Francoual (e), D.K. Shukla (e), J. Strempfer (e), T. Chatterji (f), C.M.N. Kumar (a), R. Mittal (g), H.M. Rønnow (h), C. Rüegg (i,j), D.F. McMorrow (j) and T. Brückel (a,b), Phys. Rev. B 84, 054419 (2011).

(a) Jülich Centre for Neutron Science JCNS and Peter Grünberg Institut PGI, JARA-FIT, Forschungszentrum Jülich GmbH (Germany)

(b) Jülich Centre for Neutron Science JCNS-FRM II, Forschungszentrum Jülich GmbH, Outstation at FRM II (Germany)

(c) Hefei National Laboratory for Physical Science at Microscale and Department of Physics,University of Science and Technology of China (China)

(d) ESRF

(e) Deutsches Elektronen-Synchrotron DESY (Germany)

(f) ILL, Grenoble (France)

(g) Solid State Physics Division, Bhabha Atomic Research Centre (India)

(h) Laboratory for Quantum Magnetism, Ecole Polytechnique Fédérale de Lausanne (EPFL) (Switzerland)

(i) Laboratory for Neutron Scattering, Paul Scherrer Institut (Switzerland)

(j) London Centre for Nanotechnology and Department of Physics and Astronomy, University College London (UK)

 

References

[1] Y. Kamihara et al., J. Am. Chem. Soc. 130, 3296 (2008).

[2] H. Maeter et al., Phys. Rev. B 80, 094524 (2009).

[3] W. Tian et al., Phys. Rev. B 82, 060514 (2010).