Calculating the L_2,3 XAS of Ti⁴⁺

In this tutorial, we will use the L_2,3 absorption spectrum of Ti⁴⁺ to illustrates some of the fundamental concepts in using multiplet calculations as a tool to interpret experimental data. The absorption spectrum results from the 2p to 3d electronic dipole transitions. As can be seen from the figure below the spectrum calculated using multiplet theory can be in very good agreement with the experimental spectrum (dotted).

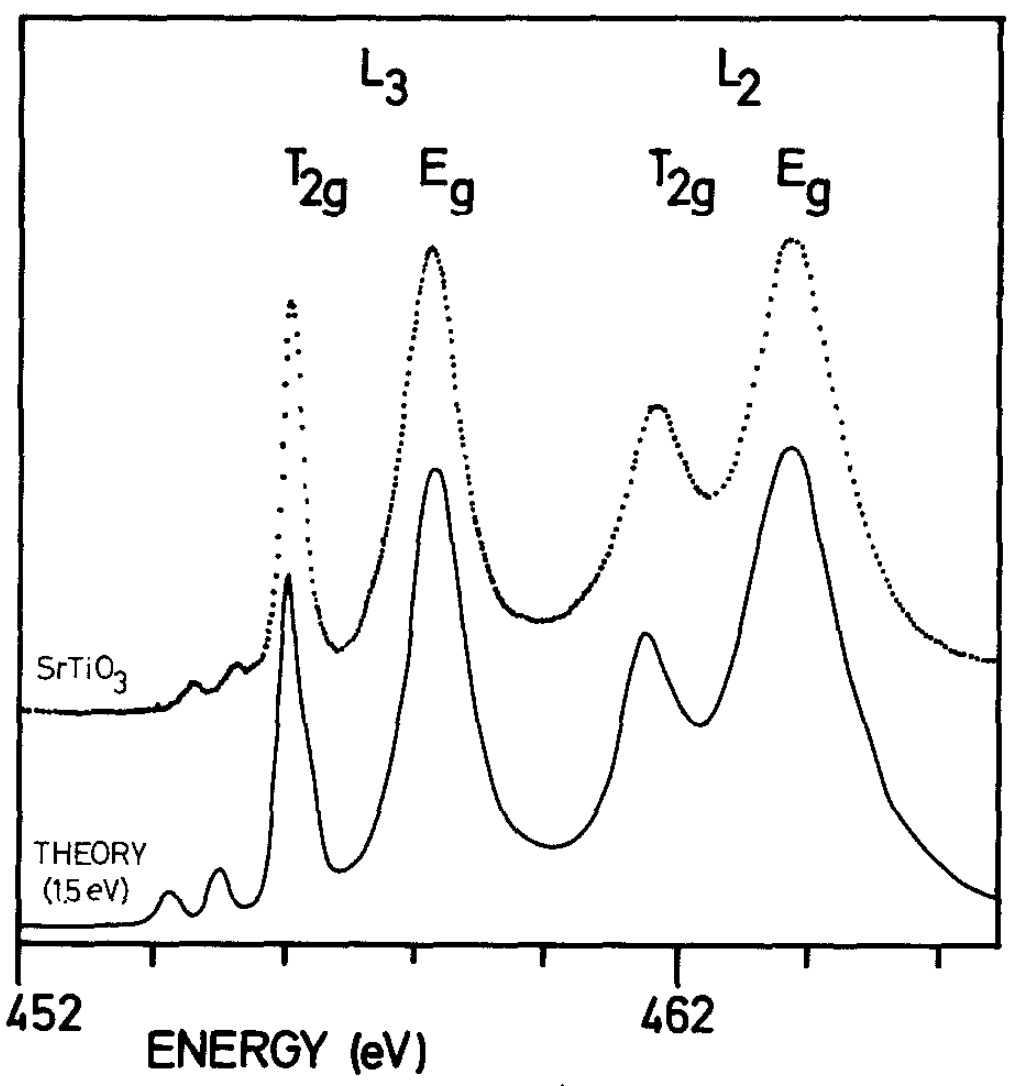
de Groot et al., Phys. Chem. Minerals, 1992, 19, 140–147.

Atomic Multiplet

1. Calculate the L_2,3 spectrum of Ti⁴⁺ in spherical symmetry, i.e. using an atomic representation of the system. For this, you need to exclude the crystal field contribution from the Hamiltonian. In addition, set the Lorentzian broadening to 0.1, and the Gaussian broadening to 0.0. Leave all the other parameters to their default values. How many transitions are visible in the spectrum? Identify the L₂ and L₃ edges.

Note: What is the initial electronic configuration of Ti⁴⁺? How many multi-electronic states does this configuration have? Write down their spectroscopic terms. Repeat the same exercise for the final electronic configuration. Using the selection rules for dipole transitions (ΔJ = 0, ±1 except for J = J‘ = 0) how many transitions do you expect?

2. In semi-empirical multiplet calculations, the Hamiltonian parameters are varied to improve the agreement with the experiment. In the case of the atomic parameters, i.e. Slater integrals and the spin-orbit coupling constants, instead of modifying the parameters themselves, it is customary to use scaling factors to change them. Run a calculation with the scaling of the 2p spin-orbit coupling constant, ζ(2p), set to 0.5. After the calculation finishes, set this value back to 1.0, and run a second calculation with the 3d spin-orbit coupling, ζ(3d), in the Final Hamiltonian set to 0.5. Which interaction affects the most the energy separation between the L₂ and L₃ edges? Check that the energy separation between the two edges is close to 3/2·ζ(2p).

3. Change back the scaling parameter to 1.0 for both 2p and 3d spin-orbit coupling. Perform three calculations using 0.8, 0.4, and 0.0 for the scaling of the Slater integrals, F_k and G_k. Instead of changing each scaling value individually as before, use the input boxes above the Hamiltonian terms. Plot the three spectra. What is the influence of the electronic repulsions on the spectrum? Check that in the last case, with the scaling factors set to zero, the intensity ratio of the L₃/L₂ also called the branching ratio, is close to 2:1.

Crystal Field Multiplet

1. Set the scaling factors for the Slater integrals back to 0.8. Enable the Crystal Field and change the 10Dq value to 2.0 eV for both the initial and final Hamiltonian. In octahedral symmetry, the crystal field splitting 10Dq is also written Δ_O. Run the calculation and compare it with the case of spherical symmetry. How many transitions do you observe at the L₃ edge? How many transitions at the L₂ edge?

2. In the previous calculation the Lorentzian broadening was set to 0.1 eV to better identify the number of transitions. Change it to 0.2 eV and run the calculation. Observe its effect on the final spectrum.

3. Run a set of calculations with 10Dq ranging from 0 to 2.0 eV, in steps of 0.5 eV. Plot the resulting spectra. What is the influence of the crystal field splitting?

4. Set the 10Dq value to 2.0 eV and switch off the Slater integrals and the 3d spin-orbit coupling. How many transitions does the calculated spectrum have? Check if their intensity ratio is close to 6:4:3:2, i.e. the theoretical ratio is given by the degeneracy of the 3d orbitals (3:2) and the branching ratio discussed before (2:1). What is the energy separation between the first two transitions? How does this compare to the energy separation between the last two transitions?

Adding Tetragonal Distortion

1. Next we are going to study the influence of a tetragonal distortion, i.e. an elongation or compression along one of the four-fold axes. Lowering the symmetry from O_h to D_4h, results in a different energy splitting of the 3d orbitals as can be seen in the figure below. The relative energy position of the orbitals depends on the distortion applied to the octahedron and is determined by two parameters Ds and Dt, in addition to the Dq parameter.

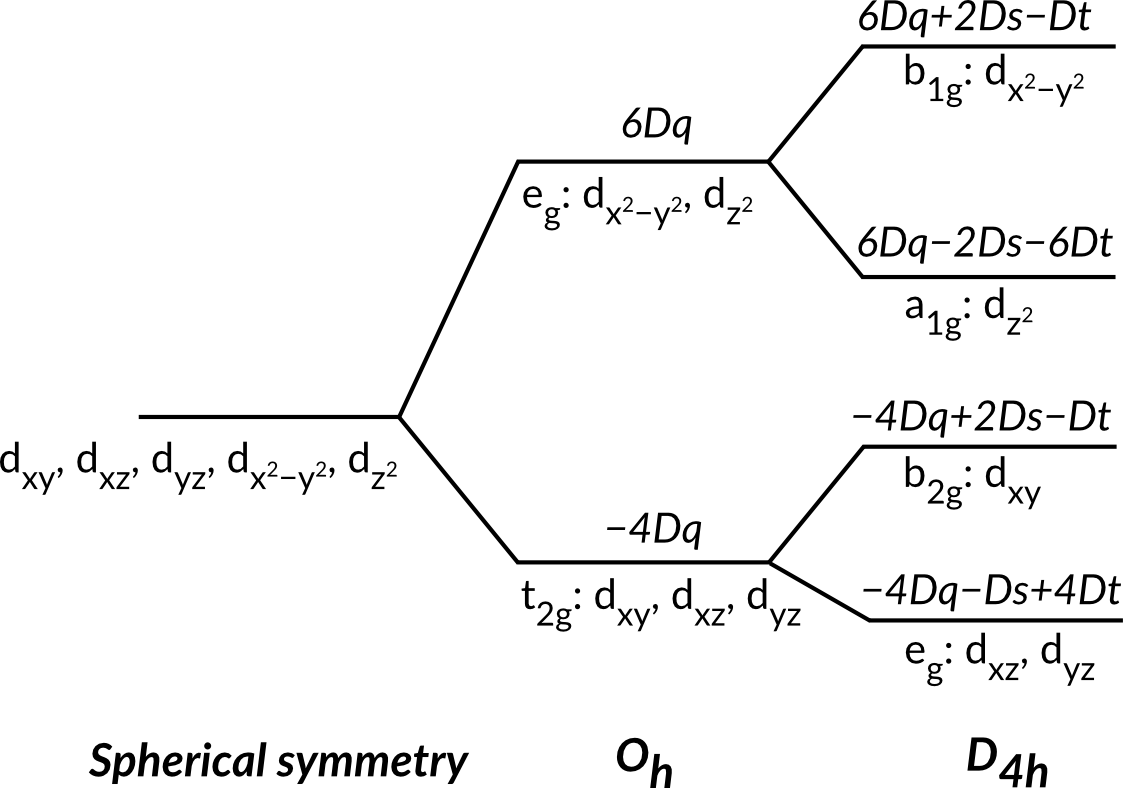
2. Change the symmetry of the system to D_4h. Note that by doing this all parameters will be reset to their default values. Set the Dq value to 0.25 eV. This is equivalent to setting the 10Dq value to 2.5 eV in the case of the O_h symmetry. While keeping Dt zero, vary the value of Ds between -0.6 and 0.6 eV in steps of 0.2 eV. Try to rationalize the changes you observe in the spectrum. Do a similar test for Dt while keeping Ds zero.