A Multiconfigurational Treatment of the L2,3 XAS in Ni2+ Compounds
The following tutorial illustrates the limitations of crystal field multiplet theory in reproducing some of the spectral features in a series of nickel compounds, and introduces the more elaborate charge transfer multiplet model, that can be used to overcome these limitations.
Crystal Field Multiplet
1. Calculate the 2p XAS spectrum of Ni2+ using the default parameters, but increase the Gaussian broadening to 0.4. Identify the L2 and L3 edges in the calculated spectrum.
2. Change the default scaling of the Slater integrals (κ) to 0.6, 0.4, and 0.2 and rerun the calculation. Overlay the four spectra and describe the evolution of the main peak and its high energy shoulder when the scaling parameter is decreased.
3. Compare the previous observation with the changes in the experimental spectra when going from fluoride to bromide in the series of nickel halides. How do the reduction factor and covalency of the metal-ligand bond correlate, knowing that the later increases with an increasing atomic mass of the halide?
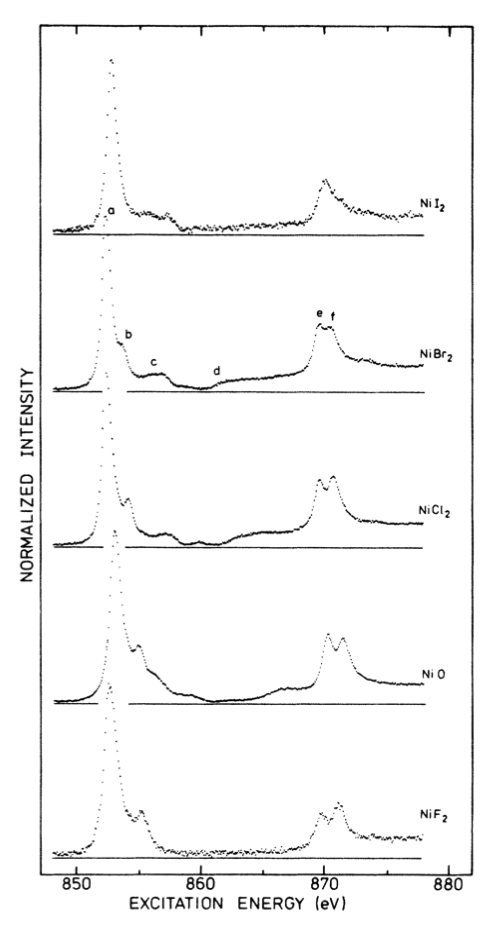
van der Laan et al., J. Phys. Rev. B, 1986, 33 (6), 4253–4263.
4. For what reduction factor do you get the best agreement with the experimental spectrum of NiBr2? Is it reasonable to have to use this scaling factor?
5. Is there a particular region of the spectrum that doesn’t seem to be reproduced using the previous crystal field multiplet calculations?
Charge Transfer Multiplet (CTM)
1. Run a calculation using the following parameters: κ = 0.9, U(3d,3d) = 7.5 eV, U(2p,3d) = 8.5 eV (Atomic), 10Dq(3d) = 0.7 eV (Crystal Field), Δ(3d,Ld) = 4.3 eV, Veg(3d,Ld) = 2.0 eV, Vt2g(3d,Ld) = 1.0 eV (3d-Ligands Hybridization). How does the calculated spectrum compare with the measured spectrum of NiO?
2. Repeat the above calculation while varying Δ between 0.0 and 10.0 eV. Notice the changes in the number of the metal 3d and the ligand electrons (<N_3d> and <N_Ld> in the logging window). What happens if Δ is negative?
3. Try to get a better agreement with the experimental spectrum of NiO by varying the crystal field parameters, 10Dq(3d) and 10Dq(Ld), and the hopping integrals, Veg(3d,Ld) and Vt2g(3d,Ld).