- Home
- News
- Spotlight on Science
- RIXS reveals signatures...
RIXS reveals signatures of propagating charge density wave excitations in cuprates
12-06-2017
The recent observation of a charge density wave (CDW) in high-Tc superconductors has raised the question of how it affects charge and lattice dynamics. In this study, using high-resolution resonant inelastic X-ray scattering (RIXS), the interference between phonons and CDW-related electronic excitations was observed for the first time in underdoped Bi2Sr2CaCu2O8+d.
Cuprates exhibit high-temperature superconductivity upon doping with charge carriers. Significant efforts have been made to uncover the underlying microscopic mechanism in high-Tc cuprates, which could ultimately lead to the synthesis of room temperature superconductors that would revolutionise the power transmission and electronics industries. However, this is a great challenge because cuprates are more complex than allowed for by the weak-coupling theoretical description established in the last century. This complexity manifests itself in the emergence of a number of different quantum phases along with superconductivity. Clarification of the interplay among these phases is necessary to gain further insight.
Recently, experimental evidence on high-Tc cuprates revealed ubiquitous charge density wave (CDW) modulations [1], which coexist with superconductivity. This is quite intriguing, since CDW, a state in which valence electrons tend to be localised, and superconductivity, a state in which electrons move freely, possess seemingly opposite electronic properties, implying a non-trivial relationship between the two. To gain further insight into this puzzling co-existence, it is necessary to uncover how CDW interplays with other degrees of freedom. In particular, some theories have also proposed that the fluctuations of CDW, i.e. a form of CDW dynamics or excitations, could be important for high temperature superconductivity [2], however, the experimental evidence of such CDW dynamics is still lacking. With sufficient energy resolution, RIXS can be an ideal probe for CDW dynamics due to its simultaneous sensitivity to excitations (and order) of charge, spin, and orbital characters [3]. The newly-commissioned soft X-ray RIXS instrument at beamline ID32 presently possesses the highest ever energy resolution at the Cu L3 edge, and thus, provides an unprecedented opportunity to tackle this challenge.
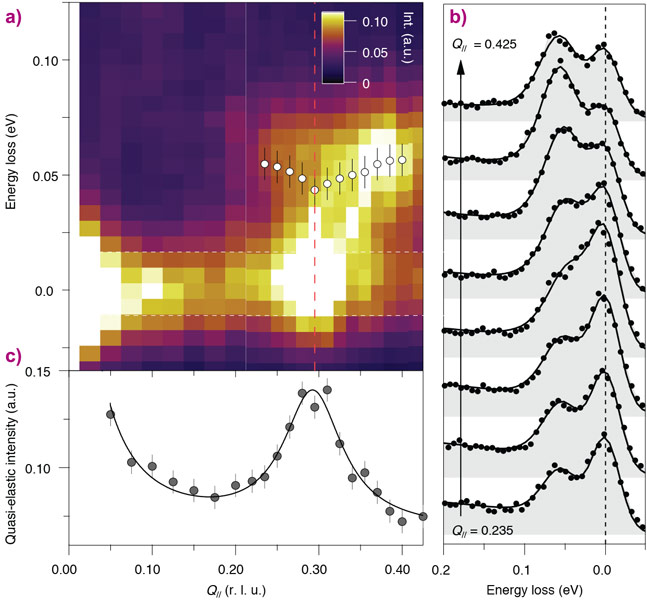
We performed high-resolution momentum-resolved RIXS on the underdoped bi-layer cuprate Bi2Sr2CaCuO8+d. Our main results are shown in Figure 1. The CDW scattering peak at QCDW ~ 0.30 r.l.u. in the quasi-elastic region and a branch of phonon excitations at ~ 60 meV, attributed as the Cu-O bond-stretching modes, are clearly resolved in the RIXS intensity map. Remarkably, the phonon intensity varies non-monotonically with momentum, having a maximum near QA ~ 0.37 r.l.u. It is important to note that the RIXS phonon cross-section directly reflects the momentum-dependence of the electron-phonon coupling strength [4], in stark contrast with the phonon self-energy measured by other techniques, e.g. inelastic neutron or non-resonant X-ray scattering. As a consequence, RIXS is also directly sensitive to the interference between phonons and underlying charge excitations, i.e. the Fano effect, which can manifest as an intensity anomaly. Thus, the intensity anomaly at QA ≠ QCDW provides evidence for the existence of dispersive CDW excitations that cause a strong Fano interference at the intersection with the bond-stretching phonon. Temperature dependence measurements and theoretical calculations of RIXS phonon cross-section were also performed to support these observations.
The dispersive CDW excitations, the phonon anomaly, and the wave vector of the CDW found in this research provide a comprehensive momentum space picture of complex CDW behaviour and point to a closer relationship with the pseudogap state. These results imply that CDW is intimately connected to the electronic structure in high-Tc copper oxides, in addition to the spin and phonon interactions. Future investigations to clarify the relationship among these underlying degrees of freedom would be crucial to uncover the mechanism of superconductivity in these materials.
Principal publication and authors
Dispersive charge density wave excitations in Bi2Sr2CaCu2O8+d, L. Chaix (a*), G. Ghiringhelli (b,c), Y.Y. Peng (b), M. Hashimoto (d), B. Moritz (a), K. Kummer (e), N.B. Brookes (e), Y. He (f), S. Chen (f), S. Ishida (g), Y. Yoshida (g), H. Eisaki (g), M. Salluzzo (h), L. Braicovich (b,c), Z.-X. Shen (a,f), T.P. Devereaux (a,f), W.-S. Lee (a), Nature Physics, accepted (2017); doi: 10.1038/nphys4157.
(a) Stanford Institute for Materials and Energy Sciences, SLAC National Accelerator Laboratory and Stanford University (USA)
(b) Dipartimento di Fisica, Politecnico di Milano (Italy)
(c) CNR-SPIN, CNISM, Politecnico di Milano (Italy)
(d) Stanford Synchrotron Radiation Lightsource, SLAC National Accelerator Laboratory, Menlo Park (USA)
(e) ESRF
(f) Geballe Laboratory for Advanced Materials, Stanford University (USA)
(g) National Institute of Advanced Industrial Science and Technology (AIST) (Japan)
(h) CNR-SPIN, Complesso Monte Sant’angelo, Napoli (Italy)
* L. Chaix has recently moved to Laboratoire Léon Brillouin, CEA Saclay (France)
References
[1] R. Comin et al., Annu. Rev. Condens. Matter Phys. 7, 369 – 405 (2016).
[2] S.A. Kivelson et al., Rev. Mod. Phys. 75, 1201 (2003).
[3] L.J.P. Ament et al., Rev. Mod. Phys. 83, 705 – 767 (2011).
[4] T.P. Devereaux et al., Phys. Rev. X 6, 041019 (2016).