- Home
- News
- Spotlight on Science
- Elastic properties...
Elastic properties revealed by thermal diffuse scattering
06-03-2017
Measurements of thermal diffuse scattering reveal that the full elasticity tensor can accurately be obtained in a single crystal diffraction experiment. This new approach allows the measurement of elastic properties together with the crystal structure.
The elasticity tensor is the fundamental quantity in the description of elastic waves in crystalline materials and it contains the full set of elastic constants. The elastic properties define mechanical properties of materials and influence phase stability. Accurate measurements of the elasticity tensor are of principal interest for the description of seismological waves and their discontinuities, which allow decisive conclusions on composition, temperature and pressure of Earth's interior. In condensed matter physics, elastic properties are important in the study of quantum phase transitions in systems with pronounced interaction of phonons with other quasi-particles. Such interactions may include electron-phonon coupling with applicability to superconductors as well as spin-phonon coupling with interesting anomalies in low-dimensional spin systems.
We now show that the full elasticity tensor can be determined by high-precision measurements of thermal diffuse scattering in a single crystal. Thermal diffuse scattering arises from the vibrations of atoms around their equilibrium positions. The result of these vibrations in a scattering experiment are intensities in-between Bragg reflections, fingerprints of the lattice dynamics. In the vicinity of Bragg reflections, the scattering intensities are dominated by acoustic phonons that correspond to elastic waves. These waves propagate with the speed of sound that can take different values depending on the crystal symmetry, direction and external influences such as temperature and pressure. The full information is given by the elasticity tensor which can be extracted by a careful analysis of the scattering intensities.
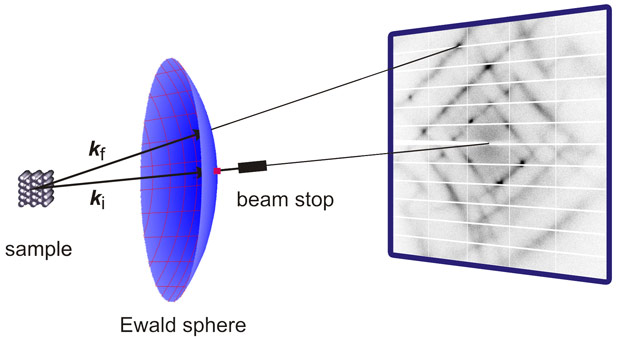
The investigated benchmark materials were high-quality single crystals of magnesium oxide and calcite. The experimental setup is illustrated in Figure 1. Scattering intensities were collected at beamlines ID29 and BM01A. The sample was rotated with small angular steps of only 0.1 degrees with exposure times adapted to the weak diffuse scattering. Measurements were taken at various temperatures. Details of the experimental setup and the underlying theory can be found elsewhere [1,2].
The data treatment required a novel analysis technique and the development of a specialised software package, which comprises the precise reconstruction of reciprocal space and careful selection of regions in reciprocal space to be treated. The software simultaneously fits approximately 107 individual intensity points by taking into account the exact scattering geometry and symmetry of the crystal. The full formalism of the fitting procedure is described in detail in the principal publication.
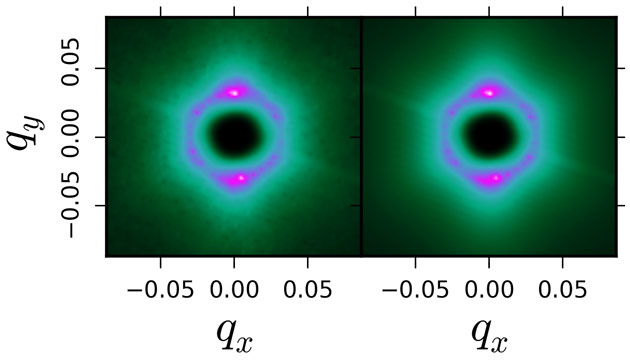
The determination of the elastic constants from thermal diffuse scattering measured at a single temperature is demonstrated for a small calcite single crystal. For the fit, scattering intensities in the proximity of the 48 most intense Bragg reflections were considered. Experimental scattering intensities and calculated thermal diffuse scattering intensities from the fitted elastic constants are compared in Figure 2, where an excellent agreement of scattering intensities can be appreciated. Remarkably, the obtained results agree within about 1% with values determined by ultrasound measurements, see Table 1.
Absolute values of the elastic constants can be obtained if measurements are taken at slightly different temperatures. This strategy further allows separation of the inelastic contribution from elastic scattering that may arise from disorder or imperfect surfaces. This is shown for magnesium oxide (see Table 1) for which accurate values in absolute units of the full elasticity tensor were obtained by fitting scattering intensities in the vicinity of 78 Bragg reflections at two temperatures.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Table 1. Elastic constants of calcite and magnesium oxide determined from thermal diffuse scattering (TDS) and ultrasound measurements (US). Values are given in GPa. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Importantly, the analysis is model-free and provides values with a precision comparable to standard methods such as ultrasound measurements of Brillouin scattering. The advantage over these techniques is that the new approach can be applied to very small and opaque crystals of arbitrary shape and symmetry. The new technique allows measurement of the elastic properties together with the crystal structure under the same experimental conditions. This implies a broad applicability of the technique in material science, geophysics and in the study of sound wave anomalies due to fundamental interactions in condensed matter physics. The proposed methodology can be extended to measurements at extreme conditions such as high pressures, high or low temperatures or high magnetic fields. The application to high pressure is particularly interesting for the establishment of absolute pressure scales in a single experiment. Temperature-dependent studies are also possible. At very low temperatures the strategy is expected to work well and would potentially be very useful in the study of spin-lattice coupling. At temperatures relevant for geophysical processes, absolute values can be obtained if the adiabatic bulk modulus is known.
Principal publication and authors
Full elasticity tensor from thermal diffuse scattering, B. Wehinger (a,b), A. Mirone (c), M. Krisch (c) and A. Bosak (c), Physical Review Letters 118, 035502 (2017); doi: 10.1103/PhysRevLett.118.035502.
(a) Department of Quantum Matter Physics, University of Geneva (Switzerland)
(b) Laboratory for Neutron Scattering and Imaging, Paul Scherrer Institute, Villigen (Switzerland)
(c) ESRF
References
[1] B. Wehinger, PhD thesis, Université de Grenoble (2013), http://tel.archives-ouvertes.fr/tel-00961602.
[2] A. Bosak et al., Journal of Physics. D, Applied Physics 48(50), 50400 (2015); doi: 10.1088/0022-3727/48/50/504003.