- Home
- Users & Science
- Scientific Documentation
- ESRF Highlights
- ESRF Highlights 2006
- Materials Science
- Competition between order and phase separation in Au-Ni
Competition between order and phase separation in Au-Ni
Binary alloys are generally classified into two generic types of ordering or phase separating character. The phase behaviour of a binary A-B system is determined by a balance between the interactions VAA, VBB, and VAB which are typically of the order of 1 eV. The resulting effective pair interaction V = VAA+VBB-2VAB, on the other hand, is typically in the order of several ten meV, and, thus, competing with the thermal excitations in the system. In turn, only the accurate determination of these interactions by experiment and first-principle calculations allow a prediction of the alloy phase stability for a given system.
In many cases the phase behaviour of a given binary alloy system can be deduced from the short range order fluctuation spectrum in the high temperature disordered phase. Ordering systems show fluctuations with a dominant wave vector k ≠ 0, while fluctuations in phase separating systems are generally characterised by a dominant wave vector k = 0 [1]. The two cases can easily be distinguished via the diffuse scattering caused by the fluctuations in the system. However, there are many systems where such a simple picture fails. Some alloy system can indeed form a phase separated ground state while the high temperature fluctuations are of both, ordering and/or clustering type [2]. The alloy system Au-Ni, which has been regarded as a model system for phase separation, has developed into a particular conflicting case. Theoretical calculations indicated competing fluctuations of ordering- and clustering-type, while experimental studies did not provide a conclusive picture of the nature of the fluctuations in the Au-Ni alloy system.
High energy X-rays are an ideal tool to map the fluctuation spectrum of binary systems. The two main characteristics of high energy X-rays are a large penetration depth in conjunction with a large Ewald sphere. This allows one to map weak diffuse scattering intensity distributions on a timescale of a few seconds in entire planes in reciprocal space using a 2D detector. The measurements have been performed in transmission geometry at beamline ID15A at X-ray energies ranging from 60 keV to 90 keV. The Au3Ni and Au3Ni2 single crystals were mounted on a heating stage in a high vacuum environment. Scattering patterns were collected in situ at elevated temperatures and from samples quenched to room temperature.
 |
|
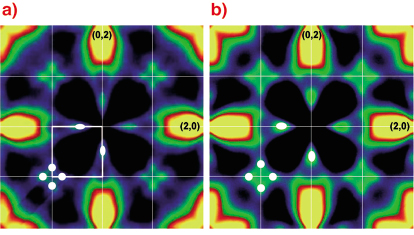
Fig. 28: Diffuse scattering in the (001) plane in Au3Ni (a) and Au3Ni2 (b). Both samples were quenched to room temperature. The positions of the diffuse scattering maxima are indicated in the lower left part. |
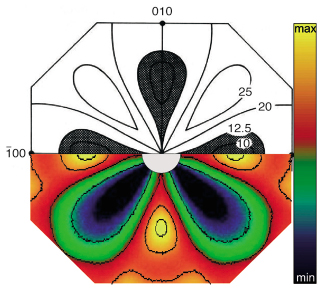
Figure 28 shows the diffuse scattering for both systems at room temperature. Several diffuse scattering maxima can be identified which demonstrate the presence of two different ordering fluctuations into the Z1 and L12 structure. The fluctuations into the phase separated state manifest themselves in the diffuse scattering intensity distribution close to the origin of reciprocal space. In Figure 29 the central part of the diffuse scattering pattern close to the origin of reciprocal space is shown together with model calculations, where both intensity distributions agree very well.
 |
|
Fig. 29: Diffuse scattering in the (001) for Au3Ni2 in the first Brillouin zone. The upper part displays model calculations, while lower part shows measured data from a quenched sample. |
Our experiments provide clear-cut evidence that the system Au-Ni exhibits a competition between ordering and phase separation. Fluctuations characteristic for ordering and phase separation have been unambiguously identified via the location of their diffuse scattering maxima. We were able to reproduce the main features of the diffuse scattering intensity distribution by first-principles calculations, thus resolving a long-standing controversy on the nature of the fluctuations in the Au-Ni alloy system.
References
[1] A.G. Khachaturyan, Theory of Structural Transformations in Solids, Wiley (1983).
[2] C. Wolverton, V. Ozolins, A. Zunger, J. Phys. Condens. Matter 12, 2749 (2000).
Principal Publication and Authors
H. Reichert (a), A. Schöps (a), I.B. Ramsteiner (a), V.N. Bugaev (a), O. Shchyglo (a) A. Udyansky (a), H. Dosch (a), M. Asta (b), R. Drautz (c), V. Honkimäki (d), Phys. Rev. Lett. 95, 235703 (2005).
(a) Max Planck Institute for Metals Research, Stuttgart (Germany)
(b) Northwestern University, Evanston (USA)
(c) Department of Materials, University of Oxford (UK)
(d) ESRF



