- Home
- Users & Science
- Scientific Documentation
- ESRF Highlights
- ESRF Highlights 2004
- Materials Science
- A New High-pressure Isostructural Phase Transition in Osmium
A New High-pressure Isostructural Phase Transition in Osmium
Recently, there has been much interest in the nature of Lifshitz [1] or electronic topological transitions (ETT). This type of phase transition arises when distortion of the electronic band structure results in a topological singularity of the Fermi surface. Interestingly, while the experimental data remain somewhat ambiguous, most simulations suggest that such an ETT in zinc does indeed exists in this pressure range. Thus, one might expect that other hcp metals should exhibit similar phenomena. Experimental and theoretical results have shown the existence of small local maxima in the band structure just above the Fermi energy near the high-symmetry point L on the zone boundary in osmium. Thus, the potential exists that these structures might fall below the Fermi energy upon compression and give rise to an ETT.
In order to clarify these points, we have undertaken an experimental study of the EoS (equation of state) of osmium using angle-dispersive X-ray diffraction with ultra-high accuracy.
Angle-dispersive X-ray diffraction measurements were recorded at the high-pressure diffraction beamline ID09A. In order to minimise the errors on the equation of state, a total of 33 diffraction patterns were recorded between 0 and 20 GPa, and 10 more points between 20 and 75 GPa in both Ne and He pressure generating media (Figure 42a).
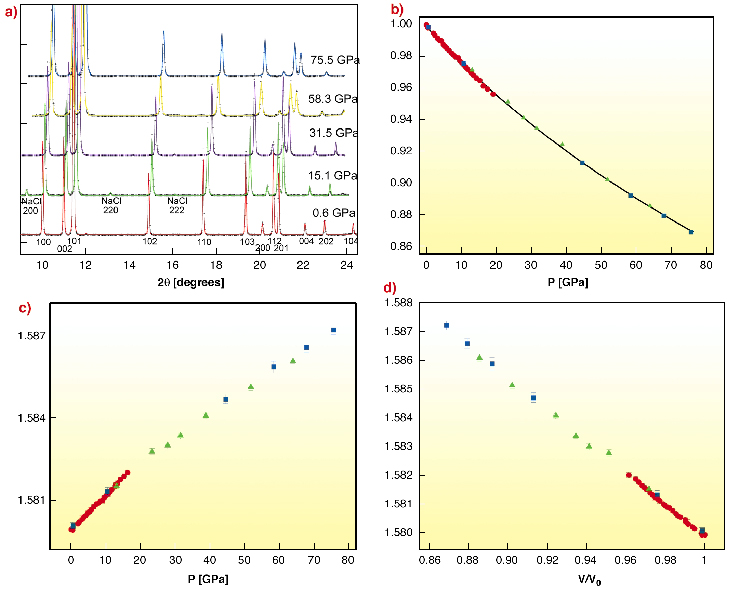 |
|
Fig. 42: a) Integrated angle-dispersive diffraction patterns recorded at various pressures. The experimental data is represented by a + symbol, and the curves are obtained from a Rietveld structural refinement of the data. The osmium reflections are labelled on the lowermost spectrum. NaCl reflections are labelled on the second spectrum. b) The isothermal equation of state of Osmium at 300 K. The different Symbols correspond to the three independent loadings (the size of the symbol is greater than the experimental errors both on pressure and volume). The solid curve is a third-order Birch-Murnaghan fit to the data yielding K0 = 410.9 ± 1.2 GPa, K0' = 3.97 ± 0.04, and V0 = 27.949 ± 0.002 A3. The c/a ratio of osmium versus pressure (c), and volume (d). The linear fits to the c/a vs. pressure data yield c/a = 1.57993 + 1.25049.10-4 P + O(P2) over the pressure range 0 to 25 GPa and c/a = 1.58071 + 8.65348.10-5 P + O(P2) from 25 GPa to the highest pressure achieved in the study. The linear fit to the c/a vs. reduced volume data yields c/a = 1.63504 - 0.0552 (V/V0) + O(V2). |
The EoS derived from our data is shown in Figure 42b using the third-order Birch-Murnaghan equation; P = 3/2K0[(V/V0)-7/3-(V/V0)-5/3]{1+3/4(K0'-4)[(V/V0)-2/3-1]}, where V is the volume, V0 is the zero pressure volume, K0 is the isothermal bulk modulus and K0' its first pressure derivative. Using a stochastic minimisation algorithm on the third-order Birch Murnaghan EoS, which gives a more robust estimate of the parameters as well as the correlation matrix in the case of incompressible materials at low volumetric compression, we find K0 = 410.9 ± 1.2 GPa, K0' = 3.97 ± 0.04, and V0 = 27.949 ± 0.002 A3. Our new results show that the bulk modulus of osmium is actually 8% smaller than that of diamond, contrary to the conclusions of Cynn et al. [2], with K0' close to 4 as is to be expected for a well-behaved incompressible material.
Our new data present a most surprising and novel result; although a simple analysis of the EoS indicates that there are no first order structural transitions, a more detailed analysis of the c/a ratio as a function of pressure (Figure 42c) shows an interesting feature around 25 GPa. Two distinct compression regimes can be identified below and above 25 GPa. Importantly, these two regimes are not resolvable as a function of volume (Figure 42d) but only as a function of pressure (Figure 42c). When plotted as a function of volume, the c/a ratio exhibits a monotonous and continuous behaviour (Figure 42d) over the entire pressure range, and can be approximated by a unique linear function within the error bars. This means that the modulus, namely dP/dV, must also exhibit the same discontinuity as seen in the function c/a (P). These effects likely arise for changes in the electronic structure on compression and could be the signature of a Lifshitz transition, where the first derivative of the compressibility presents a discontinuity at the transition pressure and the second derivative is not defined. Such transitions arise by the passage of the Fermi surface through a topologic singularity [1]. In the case of osmium, we suggest that the anomaly may arise from the passage of the maxima in band h7 below the Fermi energy with compression resulting in the collapse of the small hole-ellipsoid. Finally, our findings show the importance of high-accuracy diffraction measurements and how these types of studies on third-generation synchrotron sources can help pinpoint, isolate, and even unveil peculiar behaviour in materials that could otherwise not be observed.
References
[1] I.M. Lifshitz, Zh. Eksp. Teor. Fiz. 38, 1569 Sov. Phys. JETP 11, 1130 (1960).
[2] H. Cynn, J.E. Klepeis, C.-S. Yoo, and D.A. Young, Phys. Rev. Lett. 88, 135701 (2002).
Principal Publication and Authors
F. Occelli (a), DL. Farber (a), J. Badro (a,b), CM. Aracne (a), D.M. Teter (c), M. Hanfland (d), B. Canny (e), B. Couzinet (e), Physical Review Letters 93 (10): Art. No. 109901 Sep 3 (2004).
(a) Earth Science Division, Lawrence Livermore National Laboratory (USA)
(b) Laboratoire de Minéralogie Cristallographie (UMR CNRS 7590), Institut de Physique du Globe de Paris, Université Paris VI (France)
(c) Organization 9753, Sandia National Laboratory (USA)
(d) ESRF
(e) Laboratoire de Physique des Milieux Condensés (UMR CNRS 7602), Université Paris VI (France)



