- Home
- Users & Science
- Scientific Documentation
- ESRF Highlights
- ESRF Highlights 2008
- High resolution and resonance scattering
- Dispersion relation of an OH-stretching vibration from inelastic X-ray scattering
Dispersion relation of an OH-stretching vibration from inelastic X-ray scattering
Hydrogen bonds influence structure-property relations in a very large variety of compounds. Consequently, numerous experimental techniques are employed to study the detailed atomic arrangement and the dynamics of hydrogen bonds between R-O-H and O-R’ groups, where R and R’ represent parts of a structure, O-H represents a significantly covalent bond with a typical distance of d(OH) ~1 Å. The hydrogen bond exists between the hydrogen and the acceptor atom, with a typical distance of 1.5–1.72 Å. The dynamics of hydrogen bonds in crystals, melts, and glasses are routinely characterised using infrared or Raman spectroscopy. However, both infrared and Raman spectroscopy probe the hydrogen dynamics in the long wavelength limit and cannot provide information on the wave vector dependence of the stretching vibration. This is a significant limitation, as it prevents the elucidation of the coupling of the hydrogen dynamics to the remainder of the lattice dynamics. Due to a number of problems, such as limited flux at high energies, intrinsic limitation of the energy resolution and the large incoherent scattering cross section of hydrogen, coherent inelastic neutron scattering is not suitable for the study of the dispersion of high frequency OH stretching vibrations.
These limitations do not exist for inelastic X-ray scattering (IXS), and here we demonstrate that the dispersion relation of OH stretching frequencies can be determined by IXS. We performed experiments on diaspore, α-AlOOH, a model system to study hydrogen bonds of intermediate strength, as it has a comparatively small unit cell, simple chemistry, and is of intermediate (orthorhombic) symmetry. It has recently been studied by DFT calculations and by high-pressure single crystal X-ray diffraction up to 0.5 Mbar [1,2]. The hydrogen bond is slightly kinked, and the OH-stretching frequencies of the four symmetrically inequivalent modes at ambient pressure are centred at ~367 meV [2]. Density functional perturbation theory (DFPT)-based calculations using the CASTEP code revealed that for some wave vectors the OH-stretching vibration has an appreciable dispersion. Specifically, at reciprocal lattice points (0.5 0.5 0) and (0.5 0 0), we predicted that there are two doubly degenerate vibrations with energies of approximately 360 and 378 meV, respectively, while at (0.5 0 0.5), all four stretching vibrations have energies of ~ 361 meV.
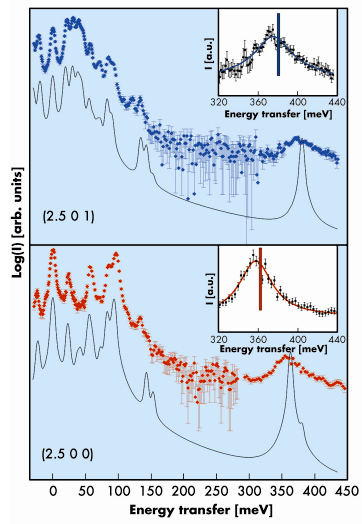
The experiment was carried out on the IXS beamline II (ID28). The instrument was operated using the silicon (8 8 8) configuration, which provides a total instrumental energy resolution of 6 meV full-width-half maximum. From a gem quality natural sample we have cut a 750 µm thick (001)-slice. The measurements were performed at ambient conditions. Counting times ranged from 60 to 2040 seconds per point. Optimal set-up parameters were determined prior to the experiment by computing theoretical spectra for a variety of wave vector transfers from the DFPT-based lattice dynamical calculations. Figure 9 shows the excellent agreement between the predicted and experimentally determined spectra. Most notably, we find mode energies of 357 (1) meV and 374 (1) meV, in excellent agreement with calculation. Furthermore the dispersion of 17 meV as a function of q was confirmed by measurements for additional reciprocal lattice points.
 |
|
Fig. 9: Predicted (line, offset for clarity) and experimental (points) inelastic X-ray spectra of diaspore at (2.5 0 1) and (2.5 0 0), both corresponding to (0.5 0 0) in reduced lattice units. For these two configurations the IXS spectra are dominated by either one or the other doubly degenerate stretching mode. The insets show an enlargement of the high-energy part of the spectrum, and the vertical bars indicate the calculated mode energy. |
An analysis of the eigenvectors (shown in Figure 10) revealed that for the high energy mode, the H-H distances remain constant during the vibration at about 2.42 Å, while for the antisymmetric low energy phonon, the hydrogens are further apart for most of the time. Hence, the H-H repulsion energy is lowered as the mode amplitude increases, lowering the potential and consequently the frequency of this mode.
 |
|
Fig. 10: Eigenvectors of the phonons at the Brillouin zone boundary at (0.5 0 0), showing that during the high frequency vibration (left) the hydrogen remain at a constant distance, while during the low frequency motion (right) the hydrogens move further apart. Purple red and white spheres represent Al, O and H atoms, respectively. |
The present experiment shows that dispersion relations at very high frequencies can be measured by IXS, thus offering new opportunities, for example, in the study of phase transformations which are governed by a change in the hydrogen bonding.
Principal publication and authors
B. Winkler (a), A. Friedrich (a), D.J. Wilson (a), E. Haussühl (a), M. Krisch (b), A. Bosak (b), K. Refson (c), V. Milman (d), Physical Review Letters 101, 065501 (2008).
(a) Geowissenschaften, Goethe-Universität, Frankfurt a.M. (Germany)
(b) ESRF
(c) Rutherford-Appleton Laboratory, Didcot (UK)
(d) Accelrys, Cambridge (UK)
References
[1] A. Friedrich, D.J. Wilson, E. Haussühl, B. Winkler, W. Morgenroth, K. Refson, and V. Milman, Phys. Chem. Miner. 34, 145 (2007).
[2] A. Friedrich, E. Haussühl, R. Boehler, W. Morgenroth, E.A. Juarez-Arellano, B. Winkler, Am. Mineral. 92, 1640 (2007).



