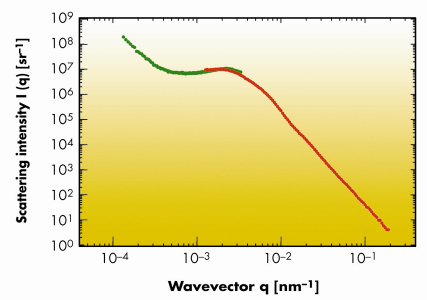
Speckles are generated whenever a scattering object is illuminated by electromagnetic radiation with a sufficient degree of coherence. In modern synchrotron beamlines the necessary spatial coherence is achieved by selecting a single coherence area of the beam. This is typically done by using a limiting aperture with size of the order of 10 µm and implies a considerable loss in terms of accessible area. For the first time, we have recently observed at BM05 that the use of limiting apertures is not necessary if one operates in the deep Fresnel [1] region (near field) of the object. The radiation emitted by the bending magnet is mildly monochromatised by a multilayer monochromator and impinges directly on the sample. The proximity of the detector to the sample guarantees the coherent superposition of the stochastically-dephased scattered waves with the transmitted beam. From this originates a speckle field with the same properties of the recently-discovered optical near-field speckles [2]. Optical near-field speckle images can be numerically Fourier transformed by getting results fully equivalent to far-field scattering experiments, where the Fourier transform takes place due to free space propagation. We report in Figure 137a a typical speckle image obtained with an area detector at about 3 cm from a cellulose acetate membrane. The background has already been subtracted and only the fluctuating part of the signal is shown. The circular symmetry of the speckles in Figure 137a and of the Fourier power spectrum in Figure 137b indicates that spatial coherence effects are negligible. Even though the principle underlying near-field experiments is wavelength independent, some additional precautions must be taken into account in the X-ray case. This is due to the strongly-uneven frequency response of X-ray area detectors and to the presence of an oscillatory transfer function caused by the Talbot effect, clearly visible in Figure 137b. After correction for these effects and azimuthal average, one is left with the scattering intensity distribution in absolute units as a function of the scattering wavevector q, reported in Figure 138, in the range [1x10–4, 4x10–3] nm–1. In the same graph we report at higher q results on the same sample obtained with a state of the art ultra small-angle X-ray scattering (USAXS) instrument, like the Bonse-Hart (BH) camera installed at ID02. We find a peak at qp = 2.3 x 10–3 nm–1 which can be associated to a characteristic size dp = 2 / qp = 2.7 µm, related to the alternating void structure in the sample.

Fig. 137: a) Speckle image recorded at about 3 cm from a cellulose acetate membrane. The background has already been subtracted and only the fluctuating part of the signal is shown. b) Two dimensional Fourier power spectrum of the image (a).

 

Fig. 138: Absolute scattering intensity I(q) for a microporous membrane with nominal pore size 0.45 µm. The red curve (high q) corresponds to data obtained with a Bonse-Hart camera. The green curve (low q) is obtained with the near field speckle method.

Additional experiments have also shown that a temporal monitoring of the near field speckles allows small-angle dynamic scattering measurements to be performed. We have tested the method on a colloidal suspension of silica particles in water. The data are in very good agreement with higher wavevectors X-ray photon correlation spectroscopy (XPCS) data taken at ID10A on the same sample.

A near field speckle based scattering experiment is experimentally simple and shares the same instrumentation with phase-contrast imaging experiments. It offers access to a wavevector region not available to existing techniques, representing therefore a useful complementary technique. A relevant benefit is also represented by the possibility of using the full beam (in our measurements 1 mm2) for dynamic measurements. This suggests the use of the method for the space-resolved investigation of the dynamics of complex fluids and other inhomogeneous systems.

 

References

[1] R. Cerbino, Phys. Rev. A 75, 053815 (2007).
[2] D. Brogioli, A. Vailati, M. Giglio, Appl. Phys. Lett. 81, 4109 (2002).

Principal publication and authors

R. Cerbino (a), L. Peverini (b), M.A.C. Potenza (a), A. Robert (c), P. Bösecke (b), M. Giglio (a), Nature Physics, accepted.
(a) Department of Physics, Università degli Studi di Milano (Italy)
(b) ESRF
(c) Stanford Linear Accelerator Center, CA (USA)