Deposition of any kind of material on a smooth surface generates roughness, i.e. the height of the individual points on the surface deviates from the mean height. The phenomenon of surface roughening is a key element in thin-film formation and knowledge about the evolution of the roughness as a function of film thickness D is crucial for many nanoscale applications. A lot of theoretical effort has been spent to predict the roughness evolution for various kinds of growth scenarios and materials. The theory of self-affine surfaces is based on the scaling behaviour of (L,D): scales as a function of the lateral probed length scale, L, as L for L << and as a function of D as Dß for L >> . The lateral correlation length scales as D1/z. In this theoretical framework each film growth mechanism can be related to a distinct set of scaling exponents , ß and 1/z which may be determined by AFM and/or X-ray scattering [1, 2].

Thin films of organic semiconducting molecules are of increasing research interest due to their promising applications in electronic devices. However, the growth of organic thin films may differ considerably from the growth of inorganic or metal films. This is to be expected because of the different substrate-film interaction, and also because organic molecules are usually not spherical and may have large extensions compared to the individual atoms used in metal or inorganic film growth.

We have investigated the roughening dynamics for thin films of a specific organic molecule, diindenoperylene (DIP), grown under ultra-high vacuum conditions (Figure 84b-d). It was shown previously that these films exhibit excellent crystalline order normal to the surface with the molecules standing essentially upright with a tilt-angle j presumably around 15°-20°, see Figure 84a [3].

 

Fig. 84: (a) The molecule DIP (C32H16) and a sketch illustrating the formation of tilt-domains; NC-AFM images for films with various thickness: (b) D = 126 Å, (c) D = 1100 Å, (d) D = 9000 Å. An analysis of the AFM images reveals a = 0.628 ± 0.05.

 

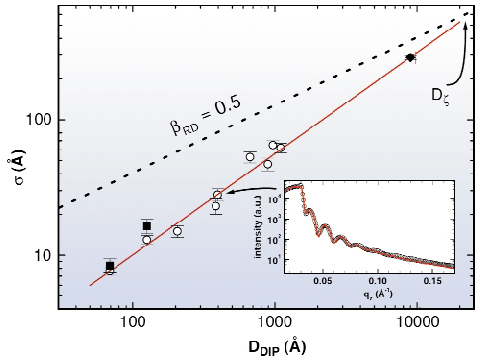
Remarkably, an unusually large growth exponent ß = 0.748 ± 0.05 of the DIP film (see Figure 85) was found in X-ray experiments at beamline ID10B. This is beyond the well-known kinetic limit for randomly deposited material D1/2. Also, 1/z = 0.92 ± 0.20 is unusually large. At present, the only model which consistently explains the rapid roughening related to the observed scaling exponents involves random spatial inhomogeneities in the local growth rate, which are fixed during the growth process.

 

Fig. 85: Log-log plot of vs. D and a linear fit to the data which gives = 0.748 ± 0.05. For D 1100 Å, X-ray-reflectivity was used to determine (O), see inset as a typical example for a sample with D = 396 Å. For some samples the saturation roughness has been determined (also) by AFM-measurements (n = OMICRON AFM, u = DI AFM). The black dotted line with slope RD = 0.5 corresponds to the random deposition limit RD, which would be reached at D = D .

 

We attribute these spatial inhomogeneities to the tilt-domains of the film (Figure 84a). The latter form as a consequence of the shape anisotropy of the individual molecules in combination with the crystalline structure of the thin film (upright standing molecules). We hope that our study will spark interest in detailed investigations into the microscopic origin of rapid roughening in organic thin films to arrive at a more thorough understanding ­ and control ­ of the growth mechanisms for this new class of materials.

References
[1] A.-L. Barabási and H.E. Stanley, Fractal Concepts in Surface Growth (Cambridge University Press, 1995).
[2] J. Krug, Adv. Phys. 46, 139 (1997).
[3] A.C. Dürr, F. Schreiber, M. Münch, N. Karl, B. Krause, V. Kruppa, and H. Dosch, Appl. Phys. Lett. 81, 2276 (2002).

Principal Publication and Authors
A.C. Dürr (a,b), F. Schreiber (a,b), K.A. Ritley (a), V. Kruppa (a), J. Krug (c), H. Dosch (a,b), and B. Struth (d), Phys. Rev. Lett. 90, 016104 (2003).
(a) Max-Planck-Institut für Metallforschung, Stuttgart (Germany)
(b) Universität Stuttgart (Germany)
(c) Universität Essen (Germany)
(d) ESRF