- Home
- Users & Science
- Scientific Documentation
- ESRF Highlights
- ESRF Highlights 2003
- High Resolution and Resonance Scattering
- Fragility of Liquids or Fragility of Glasses?
Fragility of Liquids or Fragility of Glasses?
Glasses and the glass transition stand, in the much quoted estimate of a Nobel laureate, as "perhaps the deepest and most interesting unsolved problem in condensed matter physics" [1]. In this respect, one of the most provocative aspects, concerns the slowing down of the dynamics on decreasing the temperature of the melt. When a liquid is cooled, the loss of kinetic energy leads to an ordering of the molecules which ultimately crystallise at the melting temperature Tm. However, if cooled fast enough, some materials (glass forming materials) are capable of sustaining a metastable liquid state and, upon further cooling, to freeze into a disordered glassy state at the glass transition temperature Tg<Tm [2]. Approaching this transition from the liquid side, different systems show qualitatively different temperature dependencies of the viscous flow, commonly represented in the celebrated Angell plot (Figure 12). Consequently, on a quantitative ground, liquids have been classified by introducing the term kinetic "fragility" [3]:
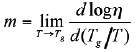
 |
|
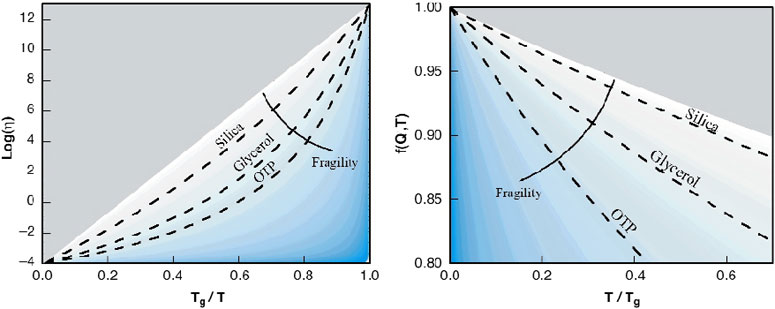
Fig. 12: (Left) kinetic fragility defined as the viscosity derivative at Tg (Angell plot); (Right) glass fragility defined as the derivative of the non-ergodicity factor at T = 0. Shaded areas (blue) indicates regions of increasing fragility, gray areas mark regions of unphysical fragilities.
|
A "fragile" liquid shows a fast change in its viscosity, when approaching the glass transition temperature (Tg) and, empirically, it is found that the fragility is related to the interaction potential (Van-der-Waals, hydrogen-bonding, covalent) among the elementary units.
The idea of looking for correlations between fragility and other quantities relevant to the glass transition is not terribly new, its importance was soon recognised as the main road to the understanding of the universality of the Angell plot. But, in the most obvious way, all the efforts have been addressed looking from the liquid side of the glass-transition.
We report here a new experimental observation relating the microscopic properties of the glassy phase to the kinetic fragility. We found that the vibrational properties in the glass away from Tg are correlated to the viscous flow in the liquid on approaching Tg.
Recent Inelastic X-ray Scattering (IXS) measurements of the dynamic structure factor have allowed the constitution of a sizeable library of high-frequency (THz) dynamical properties of glasses. Of interest here, the IXS measurements allow the determination of the non-ergodicity factor, f(Q,T), i.e. the long time limit of the normalised density-density correlation function. This quantity represents the amount of decorrelation introduced by the vibrational dynamics, and it depends on both the (T-dependent) amplitude of the vibrations and the degree of disorder of the glassy structure.
We show that the low temperature dependence of the non ergodicity factor for several glasses stands in a fashion similar to the one exhibited by the Angell plot. It is indeed possible to define a glass fragility as the derivative of f(Q,T) in the T = 0 limit (there is almost no Q dependence in the small Q region of interest here) .
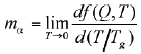
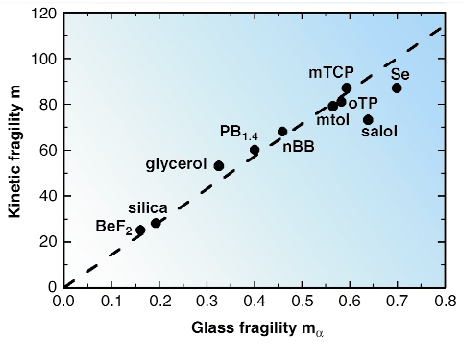
Consequently, we extend the fragility concept to the glassy state and indicate how to determine the fragility uniquely from glass properties far away Tg (Figure 13). More specifically, exploiting the harmonic approximation, one has an analytical dependence of the f(Q,T) which can be used to determine m![]() from the experimental data. Through this, we establish a way to determine the fragility of a system in the glassy phase well below Tg, independent of the way the viscosity changes with decreasing temperature from the liquid side. This conceptually surprising link between vibrational motion in glasses and diffusive processes in supercooled liquids represents a further aspect that requires clarification and, at the same time, suggests a new direction of investigation for the ultimate understanding of the glass transition phenomenology.
from the experimental data. Through this, we establish a way to determine the fragility of a system in the glassy phase well below Tg, independent of the way the viscosity changes with decreasing temperature from the liquid side. This conceptually surprising link between vibrational motion in glasses and diffusive processes in supercooled liquids represents a further aspect that requires clarification and, at the same time, suggests a new direction of investigation for the ultimate understanding of the glass transition phenomenology.
 |
|
Fig. 13: Correlation of glass and liquid fragilities for an ensemble of glass-formers. |
References
[1] P. W. Anderson, expressing a viewpoint in the journal Science, 267, 1616 (1995).
[2] P.G. Debenedetti, Metastable liquids, Princeton University Press, NJ, (1996).
[3] C.A. Angell, Science, 267, 1924 (1995).
Principal Publication and Authors
T. Scopigno (a), G. Ruocco (a), F. Sette (b) and G. Monaco (b), Science 302, 850 (2003).
(a) INFM and Universitá di Roma "La Sapienza" (Italy)
(b) ESRF



