- Home
- Users & Science
- Scientific Documentation
- ESRF Highlights
- ESRF Highlights 2000
- Electronic States and Lattice Dynamics
- Observation of Umklapp Processes in Non-Crystalline Materials
Observation of Umklapp Processes in Non-Crystalline Materials
Umklapp processes (U-processes) are scattering processes among elementary excitations in crystals where momentum conservation is fulfilled by a contribution from the lattice. Their existence has fundamental consequences on transport properties such as the finite thermal conductivity, the electrical resistivity via the electron-phonon coupling, and the electronic contribution to the heat capacity. These U-processes are understood for crystals, where they are associated with the lattice periodicity. Their existence in a topologically disordered system is a matter of debate. They are unexpected because of the absence of long-range order, but, one could also imagine that just the local order could support them, at least for those phonon-like excitations observed in disordered systems at wavelengths comparable to the inter-particle separation.
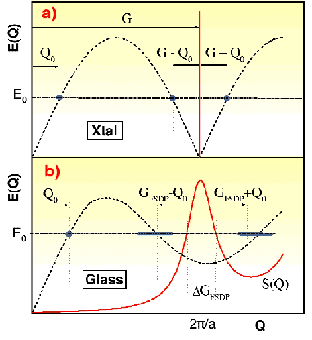 |
Fig. 69: Sketch of the dispersion relation E(Q) (dashed lines) and of the static structure factor S(Q) (red lines) of a one- dimensional system: a) reports the case of an ordered chain; b) that of a disordered chain.
|
In Figure 69a we report the one-dimensional case of an acoustic phonon dispersion relation E(Q) in a perfect chain with lattice constant a (dashed line). In such a system the dispersion relation repeats itself with a period G = 2![]() /a, while the static structure factor S(Q) corresponds to Bragg peaks at Q-values Gn = 2
/a, while the static structure factor S(Q) corresponds to Bragg peaks at Q-values Gn = 2![]() n/a (full vertical line). If we now perform a scattering experiment at the fixed energy E0, we would observe a sharp Brillouin peak, at Q = Q0
n/a (full vertical line). If we now perform a scattering experiment at the fixed energy E0, we would observe a sharp Brillouin peak, at Q = Q0 ![]() hE0/
hE0/![]() where
where ![]() is the sound velocity. This peak will also be observed at Q = G ± Q0, where G is any of the reciprocal lattice vectors; naively, one can say that the phonon of momentum Q0 is "reflected" by the lattice (or by the Bragg peak at Q = G). In Figure 69b, we report an attempt to translate one such scattering experiment from a periodic array into a disordered chain. In this case, the sharp Bragg peak is replaced by a feature, the so-called First Sharp Diffraction Peak (FSDP), centered at Q =
is the sound velocity. This peak will also be observed at Q = G ± Q0, where G is any of the reciprocal lattice vectors; naively, one can say that the phonon of momentum Q0 is "reflected" by the lattice (or by the Bragg peak at Q = G). In Figure 69b, we report an attempt to translate one such scattering experiment from a periodic array into a disordered chain. In this case, the sharp Bragg peak is replaced by a feature, the so-called First Sharp Diffraction Peak (FSDP), centered at Q = ![]() GFSDP
GFSDP ![]() 2
2![]() /a (a is the average near neighbour distance). This feature has a finite width, GFSDP, determined by the distribution of nearest-neighbour distances that typically is an important fraction of GFSDP. In analogy to the crystal case, one may expect that this FSDP is also capable of "reflecting" the phonons. However, with respect to the peak at Q0, the peaks at Q0 = GFSDP ± Q0 will have a width increased by
/a (a is the average near neighbour distance). This feature has a finite width, GFSDP, determined by the distribution of nearest-neighbour distances that typically is an important fraction of GFSDP. In analogy to the crystal case, one may expect that this FSDP is also capable of "reflecting" the phonons. However, with respect to the peak at Q0, the peaks at Q0 = GFSDP ± Q0 will have a width increased by ![]() GFSDP.
GFSDP.
IXS spectra of liquid lithium, measured as a function of Q on the horizontal spectrometer of the ID16 beamline at the indicated constant E values, are reported in Figure 70 (full circles). In the same figure the static structure S(Q) is also shown as a red line, and the FSDP is found at GFSDP ![]() 25 nm-1 with a width of
25 nm-1 with a width of ![]() GFSDP
GFSDP ![]() 4 nm-1.
4 nm-1.
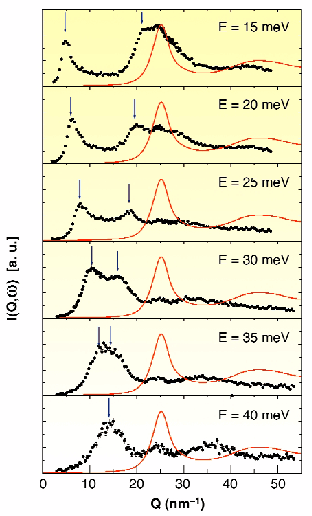 |
Fig. 70: IXS spectra of liquid lithium at T = 475 K (full circles) taken at the indicated constant energy as a function of Q. The blue arrows mark the position of the main spectral features (Brillouin peaks at low Q and Umklapp peaks around the FSDP). The red line in each panel is the S(Q) reported on an arbitrary intensity scale.
|
In the small Q region, a Brillouin peak that increases its Q position and width with increasing energy is observed. More importantly, the spectra also show other inelastic peaks at higher Q values (marked by the arrows). This ensemble of inelastic features can be interpreted within the same framework as the one sketched in Figure 69b. In fact, one observes, at low energy transfer E, not only the Brillouin peak at Q0(E), but also a second peak at approximately GFSDP - Q0(E). Moreover, one clearly observes that, with increasing E, the peaks at Q0(E) and GFSDP - Q0(E) get closer and, at the energy E ![]() 40 meV, they merge together at a Q value corresponding to GFSDP / 2.
40 meV, they merge together at a Q value corresponding to GFSDP / 2.
In conclusion, we have shown that in a system without any periodic order such as a monoatomic liquid, one observes inelastic excitations that can be interpreted as the non-crystalline counterpart of Umklapp peaks. These peaks are no longer sustained by the periodicity of the lattice as in crystals but are due to the "reflection" of the wave-like (Brillouin) excitations from the short-range order that still exists in the disordered material.
Principal Publication and Authors
T. Scopigno (a), M. D'astuto (b), M. Krisch (b), F. Sette (b) and G. Ruocco (c), cond-mat / 0010048; T. Scopigno, U. Balucani, A. Cunsolo, C. Masciovecchio, G. Ruocco, F. Sette and R. Verbeni, Europhys. Lett. 50, 189 (2000); T. Scopigno, U. Balucani, G. Ruocco and F. Sette, Phys. Rev. Lett. 85, 4076 (2000).
(a) Università di Trento (Italy)
(b) ESRF
(c) Università di L'Aquila (Italy)



