- Home
- Users & Science
- Scientific Documentation
- ESRF Highlights
- ESRF Highlights 2008
- High resolution and resonance scattering
- 3D-imaging of the Fermi surface by thermal diffuse scattering
3D-imaging of the Fermi surface by thermal diffuse scattering
The Fermi surface is one of the most important theoretical concepts in solid state physics. It is the surface in electron momentum space of a metal that separates occupied and empty electronic states. Indeed, the shape of the Fermi surface controls the electric, magnetic and thermal properties of materials. The most commonly used experimental techniques for the determination of the Fermi surface are the oscillation of transport properties in a magnetic field (i.e. the de Haas-van Alphen effect and the Shubnikov-de Haas effect) and angle-resolved photoemission spectroscopy (ARPES). Two-photon positron annihilation and Compton scattering are more indirect methods of probing the nature of the Fermi surface. Interestingly, one of the earliest techniques proposed to study the Fermi surface was to look for the abrupt variations in the dispersions of phonons [1]. These so-called Kohn anomalies arise from changes in the charge screening by the conduction electrons when the phonon wave vector q exceeds the spanning across the Fermi surface k = 2kF. Here, we exploit the fact that the phonon dispersions of a material give rise to thermal diffuse scattering (TDS) of X-rays that reflect the dispersion anomalies in characteristic intensity variations of the TDS. Using only a standard X-ray diffraction set-up and an area detector, we show that portions of the zinc Fermi surface can be visualised in three dimensions.
The experiment was performed on the Swiss-Norwegian Beam Lines (SNBL) BM01 in transmission geometry at ![]() = 0.722 Å using a MAR345 image plate. A high-quality, 30-µm-thick, zinc single crystal (MaTecK GmbH) was mounted on a rotation stage with its <110> direction a few degrees off the rotation axis. Diffuse scattering patterns were recorded with an increment of 1° over an angular range of +/- 60°. A 15-µm-thick nickel foil was used to reduce the fluorescence signal from zinc. Three-dimensional maps were reconstructed, using the CrysAlis software (Oxford Diffraction). Figure 20a shows the reconstructed diffuse scattering in the HHL plane. Two types of lens-like objects of different size are clearly visible. Larger lenses, i.e. centred around (0 0 2n) Bragg spots have the strongest intensity in the centre, whereas the smaller lens-like objects, i.e. centred around (1/2 1/2 3) appear hollow. We assign features in the intensity variation maps of the TDS to Kohn anomalies and thus to portions of the Fermi surface. To further support our interpretation, we performed ab initio calculations of the Fermi surface and the TDS patterns, using the Wien2k [2] and CASTEP [3] algorithms. As Figure 20c reveals, the large lens-like objects correspond to the inner part of the Fermi surface around the G point. The shape of the inner part of the Fermi surface makes the corresponding surface of dispersion anomaly locations (Kohn surface) just its homothetic transformation with a scaling factor 2 (q = 2kF). The hollow lens-like objects of smaller size are, in fact, just sections of the large “lenses” (see Figure 20d). Additional support is given by the modelling of the TDS intensity (see Figure 20b). While the exact shape and sharpness of Kohn anomalies are not reproduced with the CASTEP calculation, the overall resemblance in terms of contrast and intensity distribution is very convincing.
= 0.722 Å using a MAR345 image plate. A high-quality, 30-µm-thick, zinc single crystal (MaTecK GmbH) was mounted on a rotation stage with its <110> direction a few degrees off the rotation axis. Diffuse scattering patterns were recorded with an increment of 1° over an angular range of +/- 60°. A 15-µm-thick nickel foil was used to reduce the fluorescence signal from zinc. Three-dimensional maps were reconstructed, using the CrysAlis software (Oxford Diffraction). Figure 20a shows the reconstructed diffuse scattering in the HHL plane. Two types of lens-like objects of different size are clearly visible. Larger lenses, i.e. centred around (0 0 2n) Bragg spots have the strongest intensity in the centre, whereas the smaller lens-like objects, i.e. centred around (1/2 1/2 3) appear hollow. We assign features in the intensity variation maps of the TDS to Kohn anomalies and thus to portions of the Fermi surface. To further support our interpretation, we performed ab initio calculations of the Fermi surface and the TDS patterns, using the Wien2k [2] and CASTEP [3] algorithms. As Figure 20c reveals, the large lens-like objects correspond to the inner part of the Fermi surface around the G point. The shape of the inner part of the Fermi surface makes the corresponding surface of dispersion anomaly locations (Kohn surface) just its homothetic transformation with a scaling factor 2 (q = 2kF). The hollow lens-like objects of smaller size are, in fact, just sections of the large “lenses” (see Figure 20d). Additional support is given by the modelling of the TDS intensity (see Figure 20b). While the exact shape and sharpness of Kohn anomalies are not reproduced with the CASTEP calculation, the overall resemblance in terms of contrast and intensity distribution is very convincing.
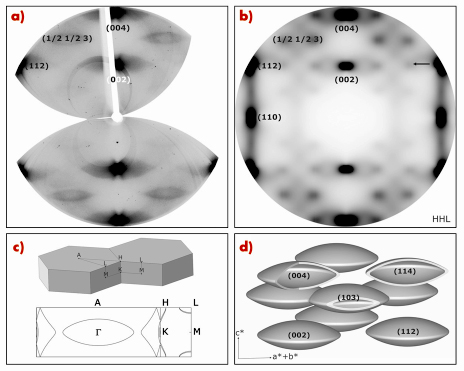 |
| Fig. 20: a) (HHL) plane reconstruction of the experimental X-ray scattering data; b) model TDS pattern derived from ab initio phonon calculations (CASTEP); c) zinc Brillouin zone and (HHL) Fermi surface section as obtained from ab initio electron band structure calculations (Wien2k); d) scheme of the assembly of lens-like Kohn surfaces centred around strong Bragg spots and their dissection by HHL planes. Experimental features not obeying the symmetry operations are experimental artifacts due to the non-linear image plate response and diffraction from the nickel filter. |
Our proof-of-principle demonstration underlines the great potential of TDS in the study of lattice dynamics and electron-phonon coupling. We have shown that the 3D-shape of the Kohn surface can be reconstructed within the timescale of hours using standard X-ray diffraction equipment. It is important to emphasise that, by using an insertion device synchrotron beamline and energy-selective area detectors, the data quality and data collection efficiency could be further increased by some orders of magnitude.
Principal publication and authors
A. Bosak (a), M. Hoesch (a), M. Krisch (a), D. Chernyshov (b), P. Pattison (b), B. Winkler (c), V. Milman (d), K. Refson (e), D. Farber (f,g), D. Antonangeli (h), submitted to Phys. Rev. B.
(a) ESRF
(b) Swiss-Norvegian Beam Lines, Grenoble (France)
(c) Geowissenschaften, Goethe-Universität, Frankfurt a.M. (Germany)
(d) Accelrys, Cambridge (UK)
(e) Rutherford-Appleton Laboratory, Chilton, Oxfordshire (UK)
(f) Lawrence Livermore National Laboratory, Livermore (USA)
(g) University of California, Santa Cruz (USA)
(h) Institut de Minéralogie et de Physique des Milieux Condensés, UMR CNRS 7590, Institut de Physique du Globe de Paris, Université Paris 6 et 7 (France)
References
[1] W. Kohn, Phys. Rev. Lett. 2, 393 (1959).
[2] P. Blaha, K. Schwarz, G.K.H. Madsen, D. Kvasnicka, J. Luitz, Wien2k, An Augmented Plane Wave + Local Orbitals Program for Calculating Crystal Properties (Karlheinz Schwarz, Techn. Universität Wien, Austria), 2001.
[3] S.J. Clark, M.D. Segall, C.J. Pickard, et al., Zeitschrift für Kristallographie 220, 567 (2005).



