- Home
- Users & Science
- Scientific Documentation
- ESRF Highlights
- ESRF Highlights 2006
- Soft Condensed Matter
- Diffusion and hydrodynamic interactions in charge-stabilised colloidal suspensions
Diffusion and hydrodynamic interactions in charge-stabilised colloidal suspensions
Charge-stabilised suspensions are ubiquitously found in chemical and waste-treatment industries, and in medical and biological products. These systems are composed of meso-scaled colloidal particles dispersed in a low-molecular polar solvent like water. Examples include proteins and viruses, paint and clay particles, and well-characterised model systems consisting of spherical latex spheres. Diffusion properties of charge-stabilised colloids are determined by a subtle interplay of electro-steric and hydrodynamic inter-particle forces. Hydrodynamic interactions (HI) are transmitted by a complicated solvent flow pattern created by the moving particles. The inherent many-body character of the long-range HI causes challenging problems in theoretical and computer simulation studies of particle diffusion.
A salient measure of the strength of HI with regard to diffusion is given by the hydrodynamic function H(q). It can be determined by a combination of static and dynamic small-angle X-ray scattering experiments. Without HI, H(q) is equal to one. Any variation in its dependence on the wavenumber q is a hallmark of HI. At large q, H(q) becomes proportional to the short-time self-diffusion coefficient DS. In earlier work [1], it was concluded that HI between charged colloidal particles are screened in the important case of a low-salt suspension. This conclusion was based on the observation of experimentally extracted values of H(q) and DS that are smaller than for a suspension of neutral hard colloidal spheres at the same concentration. The interpretation of the strong hydrodynamic hindrance in terms of hydrodynamic screening caused a controversy since, according to theory, HI screening should not occur for liquid-state suspensions of mobile particles.
 |
|
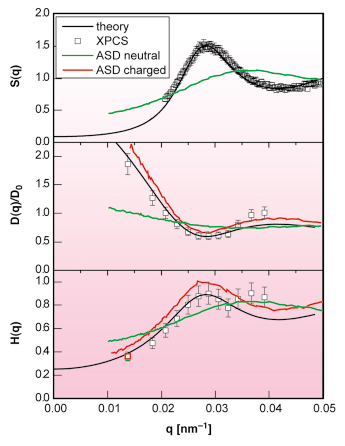
Fig. 44: Diffusion functions H(q) and D(q), and structure factor S(q), of a low-salt suspension. Experimental results (open squares) vs. ASD simulation (red lines) and theory (black lines) are shown. Green lines: simulation data for neutral hard spheres at same concentration. |
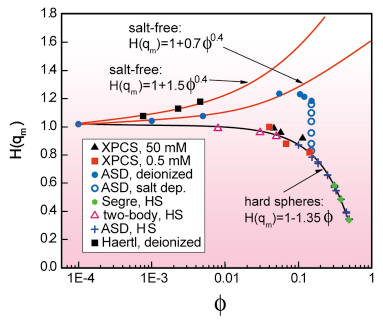
In a recent article [2], we show that, in fact, there is no hydrodynamic screening present in low-salinity systems. This important result has been obtained from combining SAXS and XPCS measurements of H(q), and of the static structure factor S(q), for aqueous suspensions of fluorinated latex spheres, with dynamic computer simulations and predictions of a modified hydrodynamic many-body theory. The XPCS experiments on aqueous suspensions of fluorinated latex spheres of radius a = 82.5 nm, with well-defined amounts of NaCl added, have been done at the ESRF’s Troika beamline, ID10A. The simulations were performed using a novel accelerated Stokesian Dynamics (ASD) method. Our simulation results for H(q) are the only ones available so far for charge-stabilised suspensions with significant many-body HI. All our experimental data on H(q), and on the collective diffusion function D(q) = D0 H(q)/S(q), where D0 is the diffusion coefficient of an isolated sphere, can be quantitatively described by the simulations, and by the modified hydrodynamic theory. In particular, the behaviour of H(q) for deionised dense suspensions can be explained by many-body HI effects, without the need to conjecture hydrodynamic screening. In addition, boundaries are provided in our study for the maximum of H(q), and for DS, over the entire range of salt concentrations. Experimental, theoretical and computer simulation results for the H(q), D(q) and static structure factor S(q) of a low-salt system are included in Figure 44. These data are compared to the simulation prediction for a suspension of neutral hard spheres of the same size and volume fraction. Figure 45 displays upper and lower boundaries for the principal peak height, H(qm), of H(q). These boundaries are approached at very small and large amounts of added salt, respectively.
 |
|
Fig. 45: Simulation and theoretical predictions for H(qm) versus volume fraction |
In conclusion, by a concerted experimental-theoretical effort, we could explain and quantify the influence of many-body HI on diffusion properties of charge-stabilised colloidal spheres. A consistent understanding of the micro-hydrodynamics of charge-stabilised spheres is important to gain improved insight into transport properties of more complex colloidal particles of interest for industry and biology.
References
[1] D.O. Riese, G.H. Wegdam, W.L. Vos, R. Sprik, D. Fenistein, J.H.H. Bongaerts and G. Grübel, Phys. Rev. Lett., 85, 5460 (2000).
[2] A.J. Banchio, J. Gapinski, A. Patkowski, W. Häußler, A. Fluerasu, S. Sacanna, P. Holmqvist, G. Meier, M.P. Lettinga and G. Nägele, Phys. Rev. Lett., 96, 138303 (2006).
[3] Härtl et al., J. Chem. Phys. 110, 7070 (1999) and Segre et al., Phys. Rev. E 52, 5070 (1995).
Principal Publication and Authors
A.J. Banchio (a), J. Gapinski (b), A. Patkowski (b), W. Häußler (c), A. Fluerasu (d), S. Sacanna (e), P. Holmqvist (f), G. Meier (f), M.P. Lettinga (f) and G. Nägele (f), Phys. Rev. Lett., 96, 138303 (2006).
(a) Facultad de Matematica, Astronomia y Fisica, Universidad Nacional de Cordoba (Argentina)
(b) Institute of Physics, A. Mickiewicz University, Poznan (Poland)
(c) FRM-II, Technische Universität München (Germany)
(d) ESRF
(e) Van’t Hoff Laboratory, University of Utrecht (The Netherlands)
(f) Institut für Festkörperforschung, Forschungszentrum Jülich (Germany)



