- Home
- Users & Science
- Scientific Documentation
- ESRF Highlights
- ESRF Highlights 2004
- Soft Condensed Matter
- Dynamic Behaviour of Magnetic Fluids
Dynamic Behaviour of Magnetic Fluids
Magnetic fluids (ferrofluids) are suspensions of colloidal particles, bearing a giant magnetic moment, in a liquid carrier [1]. These systems are interesting for both fundamental (i.e. as model systems for dipolar fluids) and applied research and find numerous applications such as in loudspeakers and hard disks.
Dynamic Light Scattering (DLS) is a well-established technique used to investigate the dynamic behaviour of colloidal suspensions. However, it has two main limitations: multiple scattering (i.e. opacity to visible light) and a limited Q-range. These constraints render any DLS investigation on magnetic fluids impossible and consequently only a few experiments have been performed addressing their dynamic properties on mesoscopic length scales.
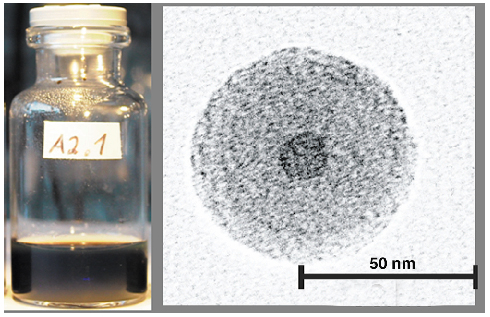
Dynamic X-ray techniques allow the limitations of DLS to be overcome. The dynamic behaviour of a novel magnetic fluid was studied on the Troïka beamline ID10A. The system investigated consists of charge-stabilised core-shell magnetic particles [2], with a CoFe2O4 magnetic core, surrounded by a silica (SiO2) shell. Figure 49 (left) shows a photograph of the opaque sample.
 |
|
Fig. 49: (left) Photograph of the sample; (right) a TEM picture of a single core-shell particle. |
The system was initially studied by small-angle X-ray scattering (SAXS) in order to characterise the core-shell structure of the colloidal composite particles and to extract the static structure factor. The effective short-time diffusion coefficient D(Q) was then probed by X-ray Photon Correlation Spectroscopy (XPCS).
For interacting systems, the contribution of direct (Van der Waals, electrostatic and eventually magnetic dipolar interactions) to the static behaviour of the system can be determined by measuring S(Q). The dynamic behaviour is described by the Q-dependent diffusion coefficient D(Q) given by
![]() (1)
(1)
where D0 is the Stokes-Einstein diffusion constant. D(Q) depends, via S(Q), on the direct interactions, but also on the indirect interactions mediated by the solvent. The indirect interactions are contained in the so-called hydrodynamic function H(Q).
The TEM image in Figure 49 (right) shows unambiguously the core-shell structure of a single particle. SAXS data provide a magnetic core-radius of 79 Å, a total core-shell radius of 356 Å and a size polydispersity of ![]() R/R = 0.13. The static structure factor S(Q) without magnetic field (o in Figure 50a ) is obtained from SAXS on a concentrated sample. The S(Q) peak indicates liquid-like ordering with a mean interparticle distance of 1550 Å. The Rescaled Mean Spherical Approximation (RMSA) was used to model S(Q), as indicated by the solid line, from which the effective number of charges per particle Z = 250 e- was determined. Hence, as far as the structure is concerned, the system can be modelled by neglecting the magnetic dipolar interactions (without an external magnetic field, the magnetic moments are randomly orientated due to thermal agitation).
R/R = 0.13. The static structure factor S(Q) without magnetic field (o in Figure 50a ) is obtained from SAXS on a concentrated sample. The S(Q) peak indicates liquid-like ordering with a mean interparticle distance of 1550 Å. The Rescaled Mean Spherical Approximation (RMSA) was used to model S(Q), as indicated by the solid line, from which the effective number of charges per particle Z = 250 e- was determined. Hence, as far as the structure is concerned, the system can be modelled by neglecting the magnetic dipolar interactions (without an external magnetic field, the magnetic moments are randomly orientated due to thermal agitation).
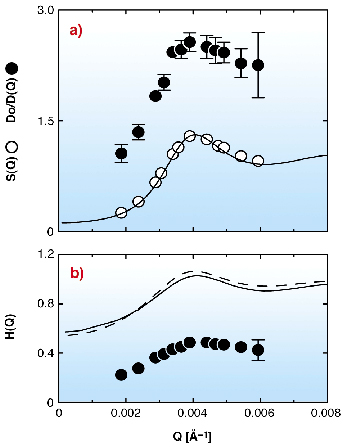 |
Fig. 50: (a) Measured static structure factor S(Q) (o). The solid line is a fit to the S(Q) using the RMSA. D0/D(Q) probed by XPCS ( |
The dynamic behaviour was probed by XPCS. Figure 50a presents the inverse normalised effective diffusion coefficient D0/D(Q) (![]() ). The diffusion constant D0 was measured to be 5.56·10-12m2s-1. D0/D(Q) displays a peak at the same position as S(Q), thus indicating that the fluctuations of the most probable configurations decay the slowest. Using the measured S(Q) and D0/D(Q), the hydrodynamic function H(Q) was extracted by Equation 1, as presented in Figure 49b. H(Q) mimics the behaviour of S(Q) and presents in particular a peak located at the same position. Over the whole measured Q-range, H(Q) < 1, indicating that the indirect interactions act as an additional friction force slowing down the dynamics.
). The diffusion constant D0 was measured to be 5.56·10-12m2s-1. D0/D(Q) displays a peak at the same position as S(Q), thus indicating that the fluctuations of the most probable configurations decay the slowest. Using the measured S(Q) and D0/D(Q), the hydrodynamic function H(Q) was extracted by Equation 1, as presented in Figure 49b. H(Q) mimics the behaviour of S(Q) and presents in particular a peak located at the same position. Over the whole measured Q-range, H(Q) < 1, indicating that the indirect interactions act as an additional friction force slowing down the dynamics.
The behaviour of the extracted H(Q) cannot be described by any of the existing colloidal hydrodynamics theories (the ![]()
![]() -expansion and pairwise additive approximation are shown in Figure 50b) and is more than a factor 2 smaller than expected over the whole Q-range. Whether or not these unexpectedly slow dynamics can be attributed to the presence of the magnetic dipoles anchored on each particle will be the subject of further investigations.
-expansion and pairwise additive approximation are shown in Figure 50b) and is more than a factor 2 smaller than expected over the whole Q-range. Whether or not these unexpectedly slow dynamics can be attributed to the presence of the magnetic dipoles anchored on each particle will be the subject of further investigations.
References
[1] E. Blums, A. Cebers and M. Maiorov, ed., Magnetic Fluids (De Gruyter, New York, 1997).
[2] T. Autenrieth, J. Wagner, R. Hempelmann, W. Härtl, A. Robert and G. Grübel, Appl. Organometal. Chem. 18, 520 (2004).
Principal Publication and Authors
A. Robert (a), J. Wagner (b), T. Autenrieth (b), W. Härtl (c) and G. Grübel (a,d), J. Chem. Phys, in print; J. Wagner, T. Autenrieth, A. Robert, W. Härtl and G. Grübel, J. Magn. Magn. Mat, in print.
(a) ESRF
(b) Universität des Saarlandes, Saarbrücken (Germany)
(c) Wallburg-Realschule, Eltmann (Germany)
(d) DESY/HASYLAB, Hamburg (Germany)



