- Home
- Users & Science
- Scientific Documentation
- ESRF Highlights
- ESRF Highlights 2003
- Soft Condensed Matter
- Counterion Distribution in Spherical Polyelectrolyte Brushes
Counterion Distribution in Spherical Polyelectrolyte Brushes
Polyelectrolytes represent a special class of polymers having ionisable groups. They are involved in many practical applications in everyday life. When suspended in water or a polar solvent, the counterions will be dissociated. The characteristic features of polyelectrolytes arise from the electrostatic repulsion between the chains as opposed to the entangled nature of their uncharged counter parts. The distribution of counterions around the polymer macroion is a long-standing issue in the physics of polyelectrolytes. A polyelectrolyte brush is formed when linear polyelectrolytes are affixed onto a planar or curved surface. Moreover, the polyelectrolyte brush represents a unique case of macromolecular self-assembly, owing to their architecture and constitution bring together various notions common in soft matter physics. Hence these systems have been studied intensively both theoretically as well as experimentally [1]. In this work, we have developed a new method to probe the spatial distribution of counterions around the colloidal macroion. The approach combines high-resolution small-angle X-ray scattering (SAXS) with the anomalous dispersion by the counterions near their absorption edge.
 |
|
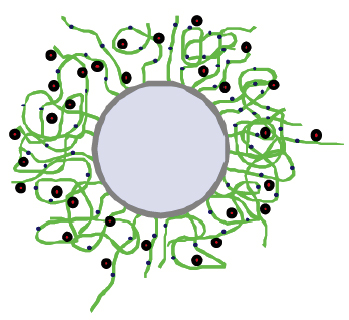
Fig. 75: Radial structure (schematic) of a spherical polyelectrolyte brush consisting of polystyrene core and chemically-grafted poly acrylic acid chains. |
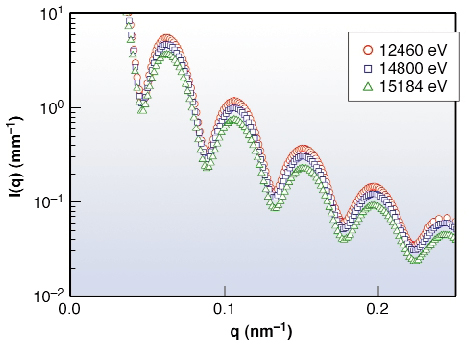
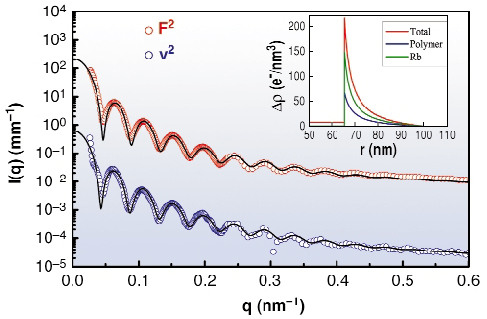
The radial structure of a brush-like polyelectrolyte is depicted schematically in Figure 75. The system consisted of dilute salt-free spherical brushes, each composed of a polystyrene core and polyacrylic acid chains chemically grafted onto the core surface. The counterions are rubidium whose K-edge falls in a convenient energy (15.2 keV) range for performing high- resolution SAXS. The measured scattered intensities become a complex function of energy near the absorption edge of the counterions. Figure 76 depicts the typical variation of SAXS intensity, I(q), as a function of scattering vector (q) in the neighbourhood of the Rb K-edge. The differential intensity scales with the known variation of the real part of the scattering amplitude (f') of the counter ions [2]. From the systematic energy dependence, the measured SAXS intensities can be decomposed into three terms: (i) the non-resonant term which corresponds to the conventional SAXS intensity removed from the absorption edge (F02), (ii) a cross-term involving the product of non-resonant and resonant scattering amplitudes (F0 v), and (iii) the resonant part of the scattered intensity arising solely by the counter ions (v2). Note that the intensity is given by the complex product of the scattering amplitudes. The key outcome of this work is that owing to high q and energy resolution, it became possible to deduce the smallest term the resonant term due to the counter ions. Figure 77 summarises the main results and shows the relative magnitudes of the F02 and v2 terms. The spatial correlation of the counter ions is directly given by the Fourier transform of v. The inset depicts the electron density profiles obtained from the decomposed scattered intensities and directly demonstrates that fine details of the spatial distribution of counterions can be obtained by the high resolution anomalous SAXS. In the polyelectrolyte brush system, the counterions are strongly correlated to the macroion. The method presented here has great potential for the analysis of charged soft matter systems.
 |
|
Fig. 76: Typical variation of SAXS intensity as the K-edge of the counterions (Rb+) is approached from below. The lowering of intensity corresponds to the decrease of the real part of the scattering factor of the counter ions. |
 |
|
Fig. 77: Decomposition of SAXS intensity into non-resonant (F02) and resonant (v2) terms. From the individual scattering amplitudes, the corresponding radial electron density profiles (inset) can be obtained. |
References
[1] A. Jusufi, C.N. Likos, and H. Loewen, Phys. Rev. Lett., 88, 018301-1 (2002).
[2] N. Dingenouts, R. Merkle, X. Guo, T. Narayanan, G. Goerigk, and M. Ballauff, J. Appl. Cryst., 36, 578 (2003).
Authors
N. Dingenouts (a), M. Ballauff (a,b), D. Pontoni (a,c), and T. Narayanan (c).
(a) Universität Karlsruhe (Germany)
(b) Universität Bayreuth (Germany)
(c) ESRF



