- Home
- Users & Science
- Scientific Documentation
- ESRF Highlights
- ESRF Highlights 2003
- Materials Science
- Crystal Structure of the Modulated Composite Arrangement of Elemental Antimony
Crystal Structure of the Modulated Composite Arrangement of Elemental Antimony
The crystal structure of the high-pressure modification Sb-II has been a long-standing matter of controversy. A conventional tetragonal solution has been suggested and refined using powder-diffraction data [1]. The resulting model comprises one type of Sb-atoms building up a three-dimensional framework and a second kind occupying every second tetragonal antiprismatic void in the resulting channels. Our investigations revealed that at pressures above 13(1) GPa pure patterns of this phase are observed. However, the correct indexing of the peak positions requires the application of the four-index method for composite structures and shows that the crystal structure comprises two tetragonal lattices with ac = 805.53(4) pm and two c-axes ch = 389.91(2) pm and cg = 297.33(4) pm. The common lattice parameter of both sub-structures is labelled ac, the c-axis of the 'host' sub-lattice is termed ch, and cg corresponds to the c-axis of the 'guest' lattice.
Beside the main reflections (hkl0) and (hk0m), the diffraction pattern contains weak first-order satellite reflections (hklm) revealing modulations of the crystal structure. The sub-structures of host atoms Sbh and guest atoms Sbg were determined and the resulting atomic positions are compatible with three different superspace groups. In two of these groups, first-order modulation waves of the Sbg positions are not symmetry-allowed. Thus, a complete refinement using full profiles including main reflections plus positions of the satellite reflections is performed in the superspace group LI422-111:LI422-111. The modulation functions for the Sbh and Sbg positions were created using a generator of the symmetry-allowed Fourier series. The refined coordinate x = 0.15776(3) of the Sbh atoms corresponds well to the value of 0.1536(3) obtained for the structurally-related modification Bi-III at 6.8 GPa [2].
 |
|
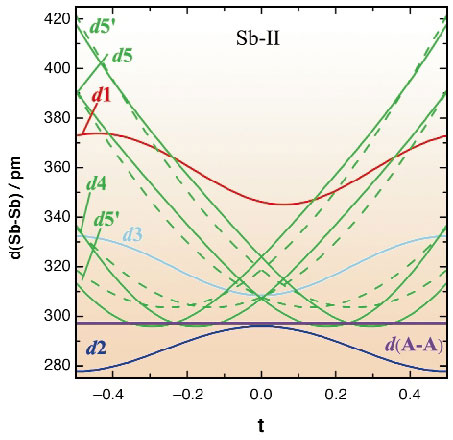
Fig. 55: Interatomic distances of Sb-II at P = 12 GPa as a function of the fourth coordinate x4. Dashed lines represent distances calculated for a non-modulated structure, full lines correspond to those of the modulated atomic arrangement, and the dotted line reproduces the distance between channel atoms. |
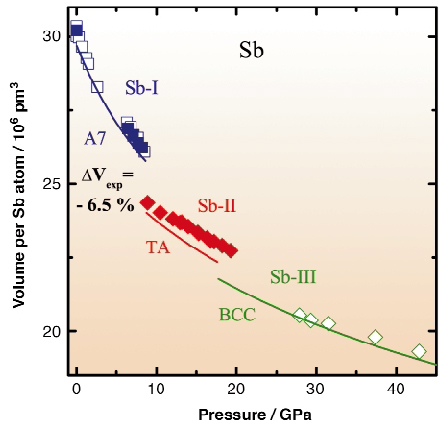
The structural pattern of host and guest atoms is commensurate along the a-axes while the arrangement of atoms within the channels and the resulting misfit causes incommensuration along the c-axes. The modulation of the Sbh atoms facilitates a continuous adjustment of interatomic distances. For the interactions among host and guest atoms, d4 and d5, the modulated displacement of antimony atoms induces an additional reduction in the regime of short interatomic contacts and an elongation at long distances (Figure 55). Within the stability region of the modification Sb-II, the axial ratio ch/cg of 1.311 (12 GPa) does not achieve the next higher rational value 4/3 which would result in a commensurate structure with the smallest possible common lattice parameter c of guest and host lattice. However, we used this commensurate model of the composite, which reproduces the basic features of the atomic organisation adequately as a model structure for the total energy calculations. The crystal structures being considered as models for the total-energy calculations were restricted to the experimentally evidenced modifications of antimony or varieties thereof. The sequence of phase transitions predicted by the calculations is in perfect agreement with the experimental findings. In order to provide a quantitative measure between experimental and theoretical results, we show a comparison between experimental and theoretical pressure-volume curves (Figure 56). Since measured and calculated volumes match almost perfectly (ambient pressure: 30.1 x 106 pm3 versus 29.7 x 106 pm3, respectively), both data sets are plotted by using absolute volumes rather than scaled values. The agreement between theory and experiment is excellent for the Sb-I phase and the Sb-III modification. Note that for Sb-II, a commensurate model is used instead of the actual incommensurately-modulated composite. Nevertheless, the transition pressure of 8.7 GPa, and the volume decrease of 5.9% (with respect to theoretical volume) are in reasonable accord with the experimental data. Only the transition pressure for the Sb-II to bcc transition is predicted to be smaller: 17.7 GPa calculated versus 28 GPa measured [3].
 |
|
Fig. 56: Volume per antimony atom at pressures up to 42 GPa. Solid symbols represent data from the present investigation; open icons indicate values taken from literature. Curved lines represent Birch-Murnaghan-type equations fitted to the results of the quantum mechanical calculations. |
References
[1] H. Iwasaki and T. Kikegawa, High Pressure Res. 6, 121 (1990).
[2] M.I. McMahon, O. Degtyareva, and R.J. Nelmes, Phys. Rev. Lett. 85, 4896 (2000).
[3] K. Aoki, S. Fujiwara, and M. Kusabe, Solid State Commun. 45, 161 (1983).
Principal Publication and Authors
U. Schwarz (a), L. Akselrud (a), H. Rosner (a), A. Ormeci (a), Yu. Grin (a) and M. Hanfland (b), Phys. Rev. B 67, 214101 (2003).
(a) MPI CPfS, Dresden (Germany)
(b) ESRF



