- Home
- Users & Science
- Scientific Documentation
- ESRF Highlights
- ESRF Highlights 2003
- Materials Science
- Structural Properties of Diamond under Hydrostatic Pressures up to 140 GPa
Structural Properties of Diamond under Hydrostatic Pressures up to 140 GPa
Diamond is the archetypical covalent material. Each atom in a sp3 configuration is bonded to four nearest neighbours. Although diamond is known as the thermodynamically-preferred allotrope of carbon at high-pressure, sufficient pressure should favour a more uniform electronic distribution and a more compact structure. The stability of diamond under pressure and the possibility of producing high-density polymorphs of diamond, including metallic forms, is still a matter of discussion but lacking reliable experimental data. Structural changes have been reported in diamond under non-hydrostatic pressures around 150 GPa and large deformation [1]. However, the measurements of the properties of diamond under hydrostatic pressure have been limited to below 40 GPa [2]. Here, we report the determination of the equation of state of diamond under hydrostatic pressure to 140 GPa. Diamond is observed to be more compressible than expected. It is also deduced that diamond remains very stable under pressure.
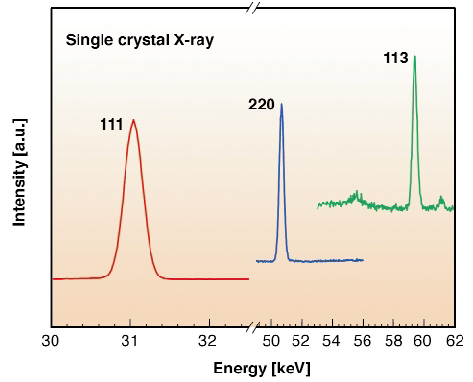
Because diamond is a very incompressible material, significant changes in the properties of diamond and detection of non-linear pressure effects require pressures in excess of 100 GPa. Such pressures are now within the capabilities of the diamond-anvil cell (DAC). The experimental difficulty in making accurate quasi-hydrostatic measurements on diamond in the 100 GPa range essentially arises because the sample chamber becomes very thin, less than 10 µm, and thus a very small diamond crystal has to be loaded, embedded in a helium-transmitting medium. Additionally, the signal of the diamond sample needs to be separated from the much larger signal of the diamond anvils. Using the ESRF synchrotron source and the energy-dispersive single-crystal X-ray diffraction technique, investigation of the structural properties of most low-Z systems have been extended into the 100 GPa range. We have used the same technique, at the ID30 beamline, to overcome the very small X-ray scattering power of a 4 µm diamond crystal [3]. Furthermore, this technique allows an easy separation of the signal of the diamond crystal and the one of the diamond anvils because of their different orientations. Three different runs were dedicated to these measurements. As shown in Figure 51, the first three classes of the diamond reflections (111), (220) and (113) were measured, and six reflections could be followed that remained perfectly correlated by the orientation matrix of the structure of diamond up to the maximum pressure. The pressure was measured by the ruby luminescence gauge (a ruby ball of 3 µm diameter was placed near the diamond crystal).
 |
|
Fig. 51: Reflections of a diamond single-crystal at 140 GPa. |
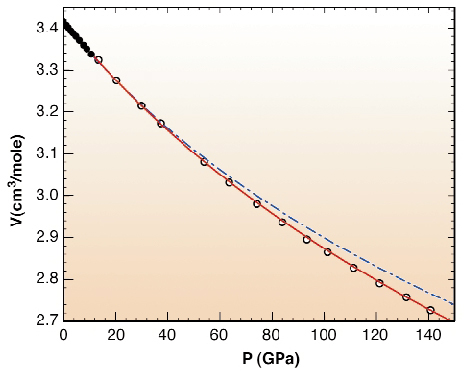
The V(P) data are presented in Figure 52. These data have been fitted by the Vinet formulation of the equation of state (EOS). It is considered to be a good formulation of the EOS and it depends on three parameters: the volume, V0, the isothermal bulk modulus, K0, and the pressure derivative of bulk modulus, K'0, at ambient pressure. In the case of diamond, it was seen that the V(P) data above 40 GPa are essential to correctly constrained K'0. Our determination of the EOS is seen to be more compressible than the one more commonly obtained by extrapolation. This is essentially due to a value of K'0 equal to 3, whereas a value of 4 is currently assumed for diamond. Complementary information was obtained with the measurement of the optical phonon of diamond at the centre of the Brillouin zone. No sign of a weakening, not even a slight increase in the covalent character, could be qualitatively deduced from the combination of the elastic data and the Raman measurements of the optical phonon frequency.
 |
|
Fig. 52: Pressure dependence of the volume of natural diamond. The dots and circles indicate respectively different runs. The error bars are smaller than the size of the symbols. The red line is the fitted Vinet equation P = 3K0(1-X)X-2exp(3(K0'-1)(1-X)/2), with X = (V/V0)1/3, V0 = 3.4170(8)cm3/mole, K0 = 446(1)GPa and K0' = 3.0(1). The blue line represents the EOS of |
In conclusion, we have observed that diamond under hydrostatic pressure is very stable. This is in contrast to its behaviour under non-hydrostatic or uniaxial compression.
References
[1] H.K. Mao, and R.J. Hemley, Nature 351, 721 (1991).
[2] Ph. Gillet et al., Phys. Rev. B 60, 14660 (1999).
[3] P. Loubeyre et al., Nature 383, 702 (1996).
Principal Publication and Authors
F. Occelli, P. Loubeyre and R. LeToullec, Nature Materials 2, 151 (2003).
CEA (France)



