- Home
- News
- Spotlight on Science
- Electronic structure...
Electronic structure of ligand orbitals revealed by valence-to-core X-ray emission
18-12-2009
The electron orbitals of ligands in 3d transition metal complexes can be studied by means of X-ray emission spectroscopy (XES). A comprehensive experimental and theoretical study of the X-ray emission from the valence band of Mn coordination complexes was carried out. The spectra provide a signature of the type of ligand and even permit a determination of the degree of ligand protonation.
Identification of ligands coordinating metal ions and understanding their electronic structure is a fundamental problem in transition metal and bioinorganic chemistry. The degree of protonation of the ligand is important for hydrolysis reactions and mechanisms of hydrolytic enzyme action. In oxidative reactions, for example in the oxygen-evolving complex of the multi-protein complex Photosystem II that is involved in the photooxidation of water in plants and cyanobacteria, the question arises whether reactive oxo-species (metal=O) exist or whether there is an oxo radical or water or a hydroxo group. The extended X-ray absorption fine structure (EXAFS) can provide valuable information on bond lengths, but is usually insensitive to H atoms and limited when distinguishing between ligands with similar atomic numbers (C/N/O). We have performed an experimental and theoretical study of the X-ray emission lines just below the Fermi level after creation of a 1s core hole (valence-to-core XES) in Mn complexes. The spectra, in connection with calculations based on density functional theory (DFT), provide information that is complementary to other spectroscopic techniques and can give valuable information on the chemical nature of metal ligands [1,2].
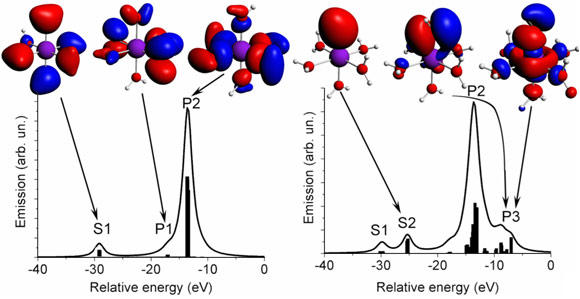
We show the calculated spectra and some important molecular orbitals that contribute to valence-to-core XES of [Mn(OH2)6 ]2+ and [Mn(OH2)5OH]+ in Figure 1. The features S and P are readily assigned to s- and p-type atomic orbitals on the O ligands. The p-orbitals form σ- or π-bonding molecular orbitals with the central Mn ion giving rise to a split feature P. Upon removal of one proton from one of the H2O ligands, the symmetry of the molecule is reduced and additional spectral features appear. Particularly interesting is peak S2 that is assigned to the O 2s orbital of the [OH]- ligand. The technique is thus sensitive to the degree of ligand protonation.
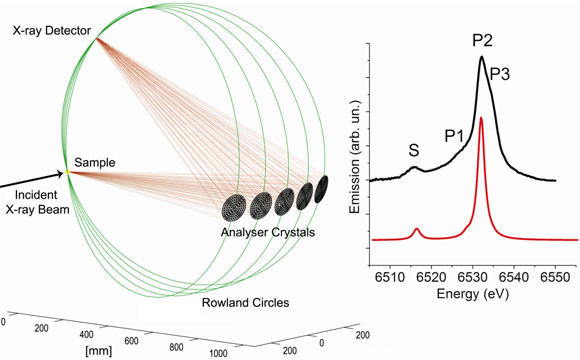
Figure 2 shows the experimental setup to measure the X-ray emission at beamline ID26. Five spherical analyser crystals select the energy and focus the beam onto a detector. An experimental spectrum for Mn2+ ions solvated in water shows reasonable agreement with the calculations for a [Mn(OH2)6]2+ cluster. The discrepancies in structure P can be attributed to structural disorder and higher coordination spheres of the solvated Mn2+ that are not considered in the calculations.
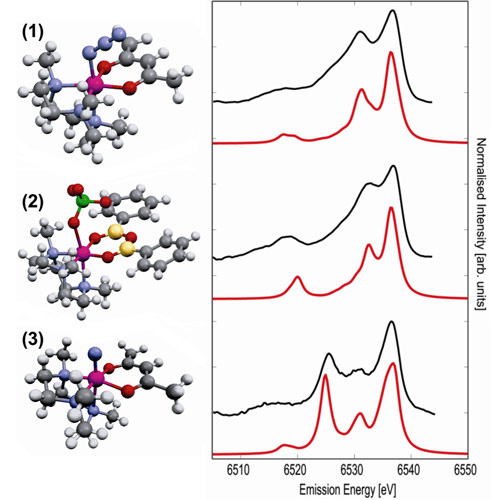
We then selected three coordination complexes (cf. Figure 3) that allowed us to study ligand substitution and oxidation state change of a Mn ion with similar metal ligands. The theoretical XES spectra are compared to experimental results in Figure 3. The overall shape of the experimental XES spectra is strongly dependent on the ligand type and oxidation state. It is very well reproduced in the calculations corroborating the validity of our computational approach. The Kohn-Sham orbitals of the density functional calculations provide the possibility to understand the origin of spectral changes on the basis of analysis of molecular orbitals that contribute to the spectral features. An important finding is that calculations for the electronic ground state, i.e. neglecting the effect of the core hole that is created during the photoionisation process, already yields good agreement between experiment and theory.
References
[1] U. Bergmann, C.R. Horne, T.J. Collins, J.M. Workman, S.P. Cramer, Chem. Phys. Lett., 302, 119-124 (1999).
[2] V.A. Safonov, L.N. Vykhodtseva, Yu.M. Polukarov, O.V. Safonova, G. Smolentsev, M. Sikora, S.G. Eeckhout, P. Glatzel, J. Phys. Chem. B 110, 23192-23196 (2006).
Principal publication and authors
G. Smolentsev (a), A.V. Soldatov (a), J. Messinger (b,c), K. Merz (b), T. Weyhermuller (b), U. Bergmann (d), Y. Pushkar (e), J. Yano (e), V.K. Yachandra (e), and P. Glatzel (f), J. Am. Chem. Soc. 131, 13161 (2009).
(a) Faculty of Physics and Research Center for Nanoscale Structure of Matter, Southern Federal University, Rostov-on-Don (Russia)
(b) Max-Planck Institute for Bioinorganic Chemistry, Mülheim (Germany)
(c) Current address: Department of Chemistry, Umeå University (Sweden)
(d) Stanford Synchrotron Radiation Lightsource, Stanford (USA)
(e) Physical Biosciences Division, Lawrence Berkeley National Laboratory, Berkeley, CA (USA)
(f) ESRF
Top image: A spectral signature for ligand orbitals