- Home
- News
- Spotlight on Science
- Colloidal Discs...
Colloidal Discs Trade their Order
14-09-2005
Every child playing with blocks knows how difficult it is to build a wall or a tower using blocks that are slightly different. A similar problem is known in self-organisation of colloids. For example, colloidal hard spheres usually fail to crystallise if their size polydispersity sigma approaches ~ 10%. Surprisingly, thin colloidal discs with a size variation of sigma > 20% can overcome this problem and easily self-assemble into columnar liquid crystals [1], which seem to be well ordered at a first glance. Now, results obtained at the CRG beamline BM26 "DUBBLE" unravel the secret of such discotic colloids.
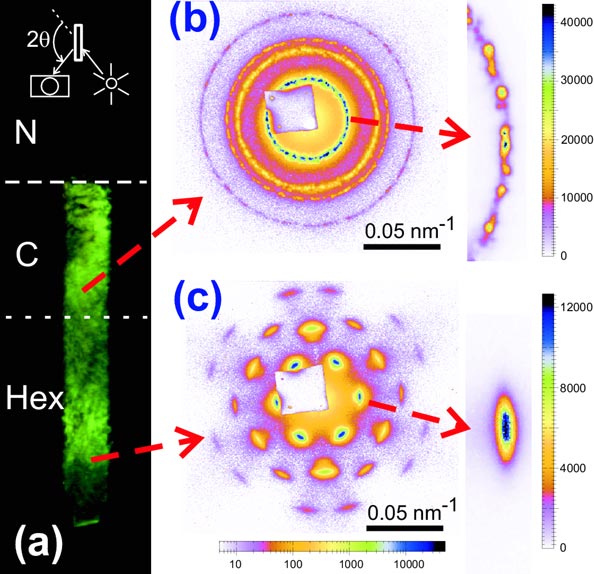
Flat glass capillaries were filled with the colloidal suspension and stored vertically. Gravity induces a monotonic increase of the osmotic pressure towards the bottom of the capillary allowing the observation of various coexisting phases within one sample. At the bottom a columnar phase yielding strong Bragg reflections of visible light can easily be identified (Figure 1a). High-resolution small-angle X-ray scattering (SAXS) shows the presence of a multidomain columnar region (Figure 1b) on top of a large (one centimetre high) single-domain columnar crystal (Figure 1c).
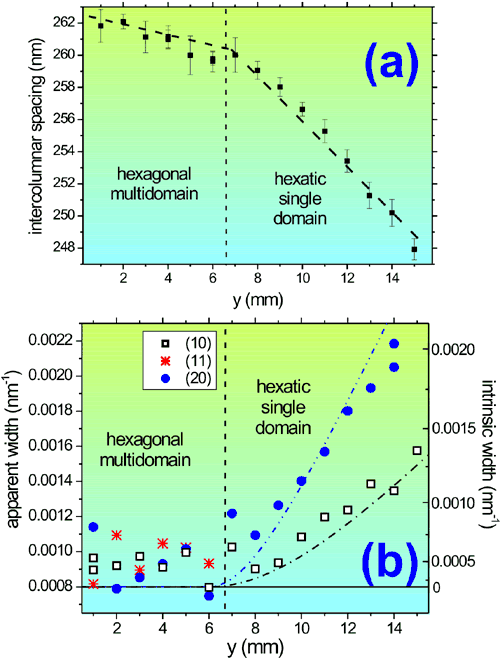
The recently improved angular resolution of BM26 [2] allowed both clear resolution of the pattern and characterisation of the reflection widths. Surprisingly, the reflection width in the radial direction is clearly broader in the single domain and it strongly increases with the diffraction order, i.e. the structure does not have an average lattice [3] and only short-range translational order is present. At the same time, the bond orientations (i.e., directions to the neighbouring columns) are well preserved over a macroscopic distance. The columns form therefore a hexatic structure. In addition to the difference in the order parameters, the compressibility of the hexatic phase is also distinctly different from that of the multidomain (Figure 2a). As shown in Figure 2b, the higher compressibility of the single domain is achieved at the cost of further reduction of the translational correlation length.
Thus, polydisperse discotic colloids form a novel phase with hexatic intercolumnar structure under gravity-induced compression. Here the long-range order is compromised in order to solve the problem of the polydispersity-induced local frustration. Colloidal discs trade off their perfect periodicity for the bond-orientational order. The higher flexibility of the hexatic phase allows the spontaneous formation of macroscopically-large monodomain liquid crystals out of highly diverse building blocks. Translating the finding to the language of the child: nature finds a way to build a sufficiently straight construction without keeping perfect repetition of the non-identical blocks.
References
[1] F. M. van der Kooij, K. Kassapidou and H. N. W. Lekkerkerker, Nature, 406, 868 (2000).
[2] A. V. Petukhov et al., ESRF Newsletter, 38, 19 (2003).
[3] A. Guinier, X-ray diffraction in crystals, imperfect crystals and amorphous bodies (Dover, 1994).
Principal Publication and Authors
A. V. Petukhov (a), D. van der Beek (a), R.P.A. Dullens (a), I.P. Dolbnya (b,a), G.J. Vroege (a) and H.N.W. Lekkerkerker (a), Phys. Rev. Lett., 95, 077801 (2005).
(a) Van 't Hoff Laboratory for Physical and Colloid Chemistry, Utrecht University (The Netherlands)
(b) DUBBLE CRG, ESRF