- Home
- Users & Science
- Scientific Documentation
- ESRF Highlights
- ESRF Highlights 2009
- Electronic structure and magnetism
- Charge localisation and orbital glass state in multiferroic LuFe2O4
Charge localisation and orbital glass state in multiferroic LuFe2O4
New materials that exhibit strong magnetoelectric coupling are fascinating because a large coupling between ferroelectric and magnetic interactions is rare, and its origin often unclear. The properties of such materials make them extremely useful in devices where the coexistence of both charge and spin components can be exploited and one property can be used to drive the other. For instance, the electric manipulation of magnetic fields could provide much faster information storage and retrieval in hard disks, since it is easier and much faster to switch an electric field than a magnetic field. Another example is memory storage, where coupled charge and spin properties allow the storage of n2 bytes at the space of n bytes; hence 1 Gigabyte would be replaced by 1 Exabyte of information in a similar space.
In most ferroelectric materials, electric polarisation arises from covalent bonding between anions and cations or the orbital hybridisation of electrons. Alternatively, ferroelectric polarisation may arise from frustrated charge order as reported for LuFe2O4. This compound is of particular interest because, in addition to ferroelectricity, magnetism originates from the same Fe ions and this holds the promise of strong magnetoelectric coupling. The ferroelectric and magnetic order takes place at and near ambient temperature which provides the potential for room temperature multiferroics.
With resonant X-ray Bragg diffraction (RXD) we investigate the electronic order of the Fe ions in LuFe2O4, using polarisation dependence and element specificity to distinguish various ordering phenomena and order parameters.
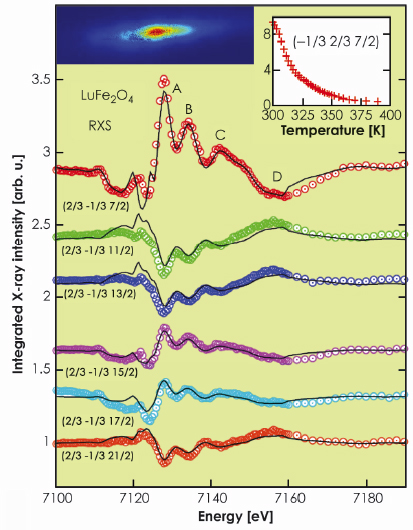
Figure 91 shows the Fe K edge resonance of several superlattice reflections characterised by wavevector (1/3 1/3 1/2). Their intensities gradually disappear above the charge ordering temperature (see inset). Non-resonant scattering associated with the crystallographic distortion that accompanies the ferroelectric polarisation dominates the diffracted intensity before and after the edge. The anomalous diffraction of the Fe ions adds phase shifted contributions to the scattering amplitude resulting in enhanced or decreased intensity at the K-edge. The solid curves in Figure 91 are the result of a fit of the data with Fe2+/Fe3+ charge order.
 |
|
Fig. 91: Integrated resonant diffraction intensity of the charge order (2/3 -1/3 l/2) reflections recorded with 2D detector at the MS beamline at the SLS at T = 15 K (see inset top left for l = 11), corrected for background, polarisation, absorption and sample geometry, normalised (shifted for clarity) and compared to charge order model described in the text. The inset (top right) shows that the superlattice intensity gradually disappears at the ferroelectric ordering temperature. |
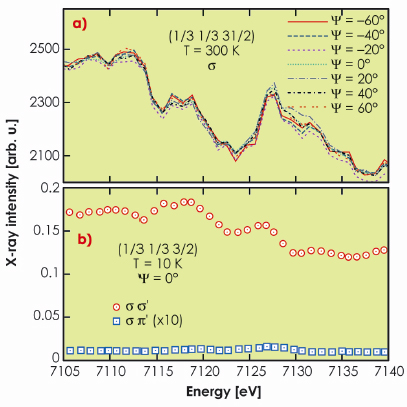
Fe3+ with five 3d electrons is close to spherical while Fe2+ with six 3d electrons exhibits doubly degenerate orbital degree of freedom, which is expected to give rise to small lattice distortion and orbital order of the Fe2+ orbitals. However, such orbital order is not observed. Figure 92 shows that the polarisation of the light does not rotate during the diffraction process and that magnitude of the resonance is independent of the orientation of the crystal. This demonstrates that the Fe2+ orbitals have random orientations. These findings of an orbital glass state are in agreement with calculations of Nagano [1].
 |
|
Fig. 92: XRD recorded at ID20. a) Intensity of the (1/3 1/3 31/2) reflection as function of azimuthal angle. b) Intensity of the (1/3 1/3 3/2) reflection with unrotated polarisation ( |
Orbital order plays a major role in the electronic properties of transition metal oxides, including magnetoresistance, metal insulator transitions and magneto-electric coupling. The appearance of an orbital glass-like state is very rare and truly interesting because it is a novel and very poorly studied electronic ground state. This state has significant consequences for the magnetoelectric properties. The orientation of the orbitals determines the magnetic exchange interactions and is part of the intricate coupling between charge and spin.
Reference
[1] A. Nagano, M. Naka, J. Nasu, and S. Ishihara, Phys. Rev. Lett. 99, 217202 (2007).
Principal publication and authors
A.M. Mulders (a,b), S.M. Lawrence (a), U. Staub (c), M. Garcia-Fernandez (c), V. Scagnoli (d), C. Mazzoli (d), E. Pomjakushina (e,f), K. Conder (e) and Y. Wang (g), Phys. Rev. Lett. 103, 077602 (2009).
(a) Department of Imaging and Applied Physics, Curtin University, Perth (Australia)
(b) The Bragg Institute, ANSTO, Lucas Heights (Australia)
(c) Swiss Light Source, Paul Scherrer Institut, Villigen (Switzerland)
(d) ESRF
(e) Laboratory for Developments and Methods, PSI, Villigen (Switzerland)
(f) Laboratory for Neutron Scattering, ETHZ & PSI, Villigen (Switzerland)
(g) Department of Applied Physics, The Hong Kong Polytechnic University (China)



